Nos quedamos sin justificar en un texto anterior (lo explicamos pero no lo demostramos) que los números reales no se pueden contar, es decir, que para cada número real no podemos asignar un número natural 1, 2, 3, 4, … ¡Vamos a ello!

De entrada, probemos que |(0,1)|=|R|, es decir, que el número de elementos del intervalo (0,1) es el mismo que el del conjunto de los números reales R. Esto es tan «fácil» como establecer una correspondencia uno a uno entre el intervalo (0,1) y el continuo de los números reales R. Para ello basta parametrizar la siguiente función:

Primero cogemos el intervalo (0,1) :

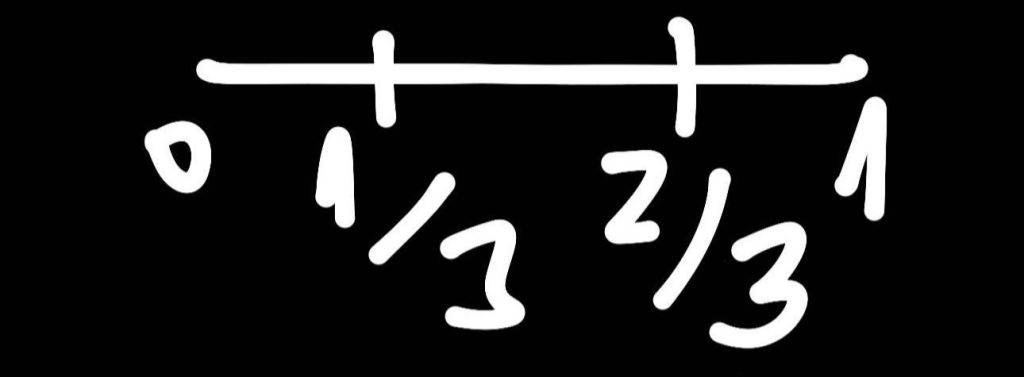
Doblamos el intervalo así:

Finalmente establecemos la correspondencia con el contínuo de los números reales R de la siguiente manera:

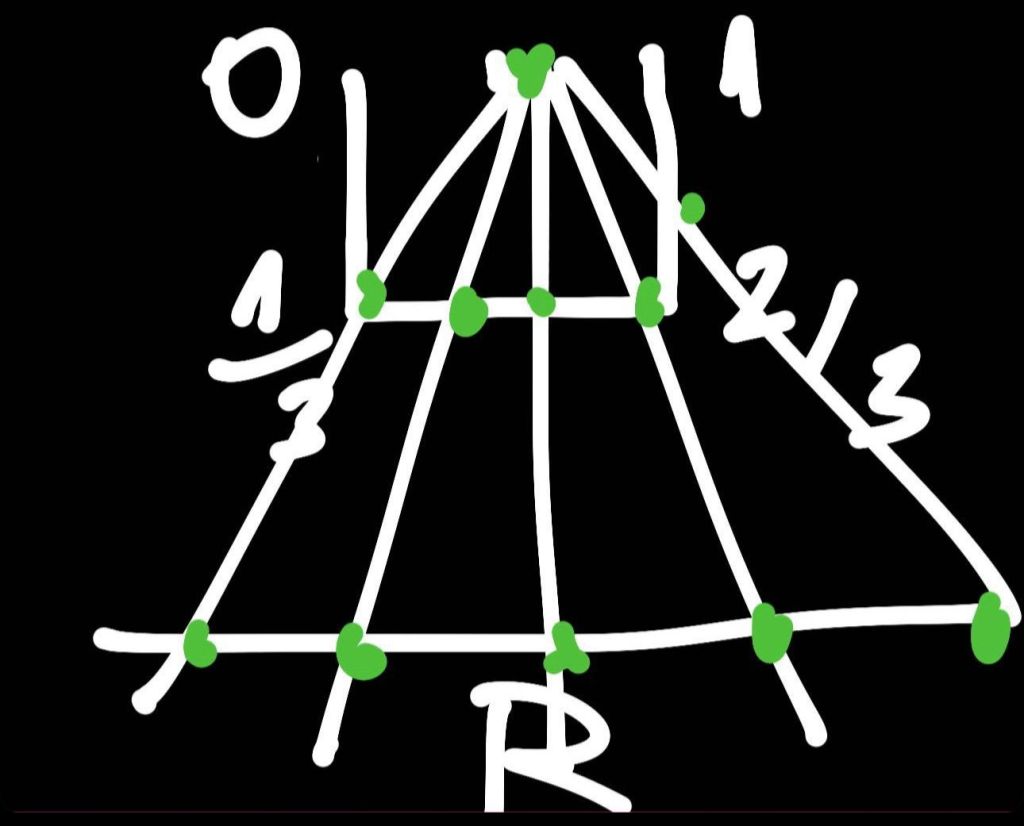
Como puede verse, a cada punto del intervalo (0,1) corresponde un punto del contínuo de los reales R y viceversa. Esto es lo que se llama función biyectiva. Ya tenemos |(0,1)|=|R|.

Ahora, dada esta función biyectiva, es decir, dada la correspondencia uno a uno entre números en el intervalo (0,1) y los números reales, demostrar que no se pueden contar los números del intervalo (0,1) equivale a demostrar que no se pueden contar los números reales R.

Consideremos una cuenta cualquiera del intervalo (0,1), esto es, una función cualquiera entre los número naturales N y (0,1):

Para obtener un número que jamás entrará en esta cuenta cualquiera basta considerar el número que se obtiene de sumar uno a cada decimal sucesivo de los números del intervalo (0,1) considerados en la cuenta anterior:

Esta sencilla pero genial idea se le ocurrió al matemático Georg Cantor. Por ello se denomina método de la diagonalización de Cantor.

En conclusión, no hay cuenta de los números reales, los números reales no se pueden contar.

Lo más interesante, no obstante, es que la matemática de Cantor permite poner de manifiesto algo que rebasa a las matemáticas mismas, a saber, la imposibilidad de simbolizar lo real. El significante puede señalar a lo real mismo en la forma de sus lapsus; en este caso, en el esfuerzo de formalización significante que supone la cuenta se apunta a un resto que no se alcanza y que, paradójicamente, se muestra a través del fallo de la cuenta; pero, insistimos, ese real mismo no puede ser simbolizado pues no puede ser contado, ergo no entra en la cuenta.

ENM (2023)