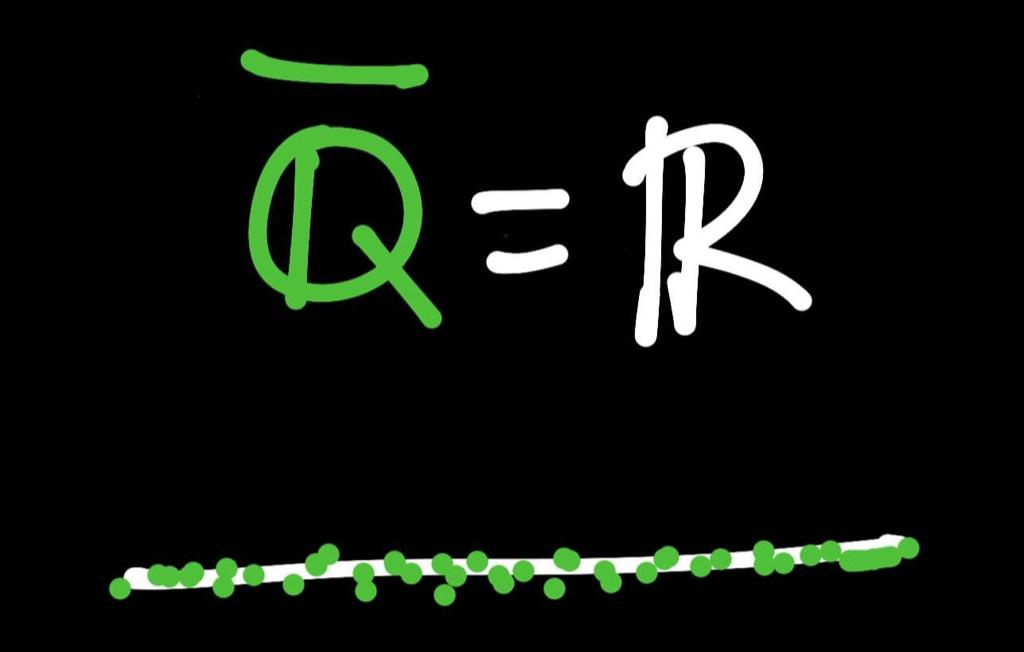
En una entrada anterior hemos demostrado con Cantor que, entre la recta infinita de los números reales R -también llamada el continuo- y el intervalo (0,1), hay una correspondencia de uno a uno. Por lo tanto, el cardinal o la cantidad de elementos del continuo y de (0,1), siendo ambos infinitos, es la misma, lo que escribíamos |R|=|(0,1)|.

Esto es sumamente sorprendente por poco que lo pensemos, pues muestra que el cardinal de todo el continuo R es igual al de una parte suya, a saber, el de (0,1).

También vimos con Cantor que los números racionales Q, a diferencia de los números reales R, son contables, luego teníamos que |N|=|Q|<|R|. Dicho de otra manera, el infinito de los racionales es menor que el de los reales y que, no obstante esto sea así, Q es denso en R.

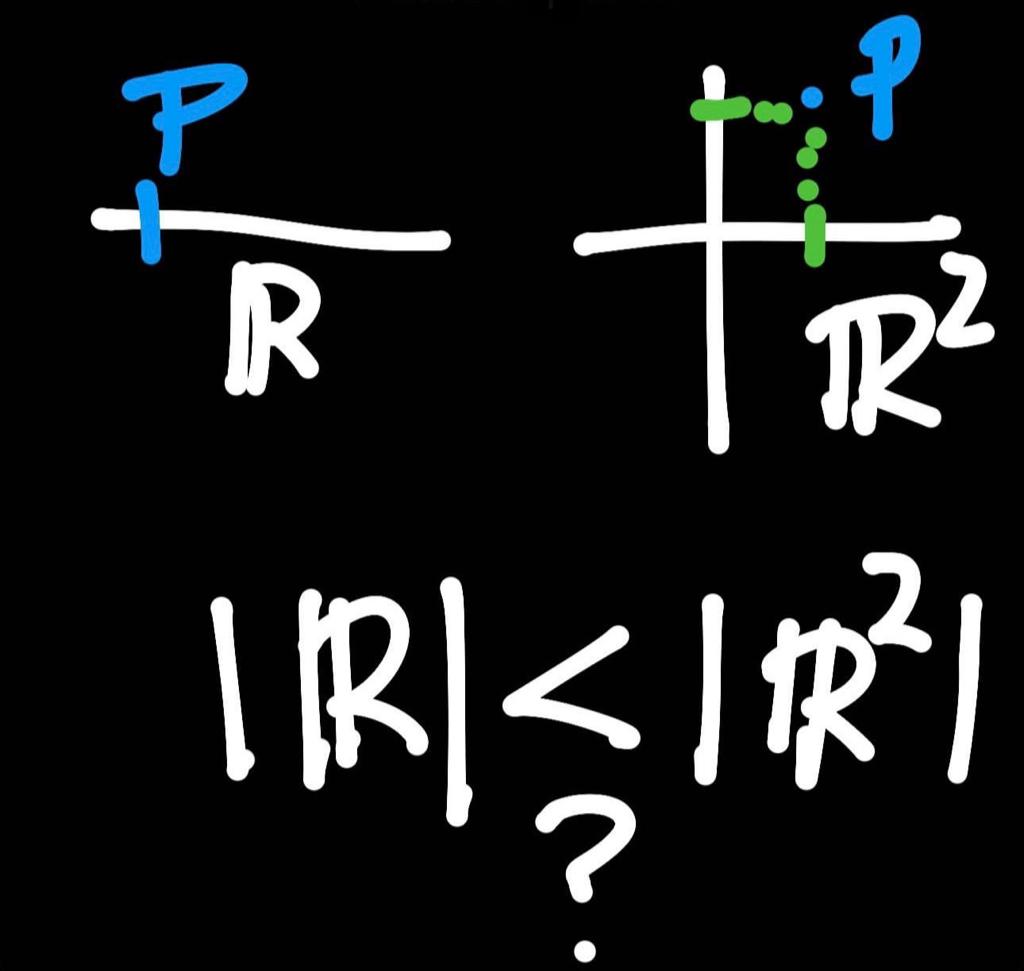
Llegados a este punto Cantor se preguntó: ¿Existe un conjunto A de números cuyo infinito sea superior al del continuo de los números reales R? Dado que hay un conjunto Q tal que |Q|<|R|, igual existe un conjunto A tal que |R|<|A|. Y lo primero en que pensó Cantor fue en el plano continuo de infinitos puntos R².

Ahora bien, igual que se puede establecer una correspondencia de uno a uno entre el continuo R y el intervalo (0,1), también puede establecerse una correspondencia de uno a uno entre el plano R² y el cuadrado (0,1)x(0,1).

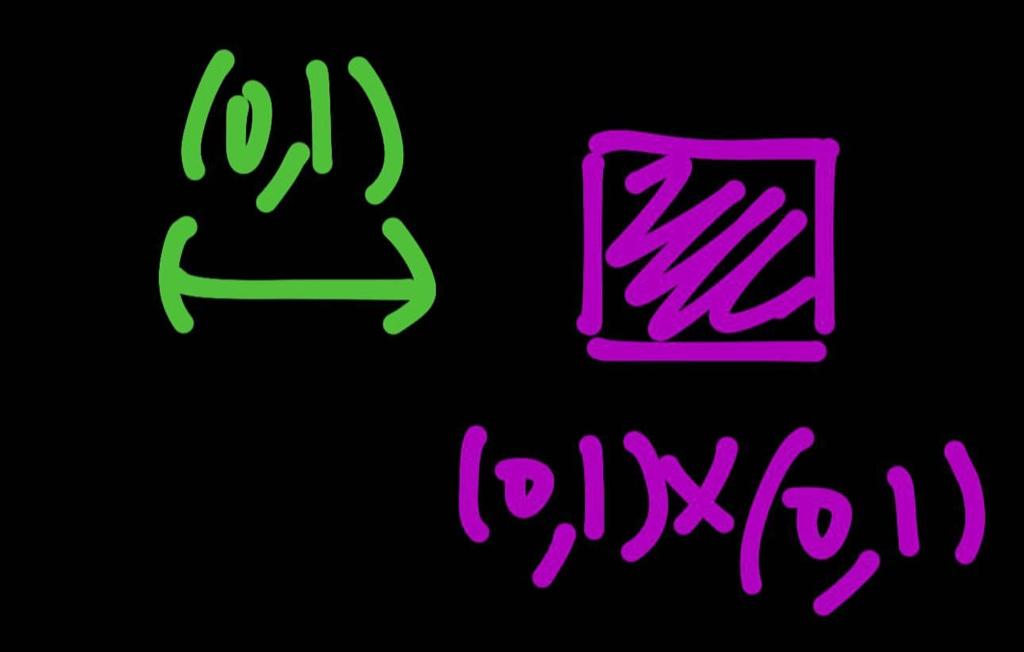
La pregunta ahora es: ¿el infinito de (0,1) es menor que el infinito de (0,1)x (0,1)?, esto es, ¿|(0,1)| < |(0,1)x(0,1)|?

Respuesta: NO, ¡son infinitos de igual tamaño!

Y ello porque se puede establecer una correspondencia de uno a uno entre los puntos del intervalo y los de cuadrado. ¿Cómo? De la siguiente manera: Para cualquier número de (0,1), por ejemplo 0,456325…, bastará asociarle, un número del cuadrado (0,1)x(0,1) de forma que tenga por abcisa los decimales en las posiciones impares y por ordenada los decimales de las posiciones pares, luego en nuestro ejemplo quedaría (0,462…, 0,535…).

De hecho, se puede demostrar que:

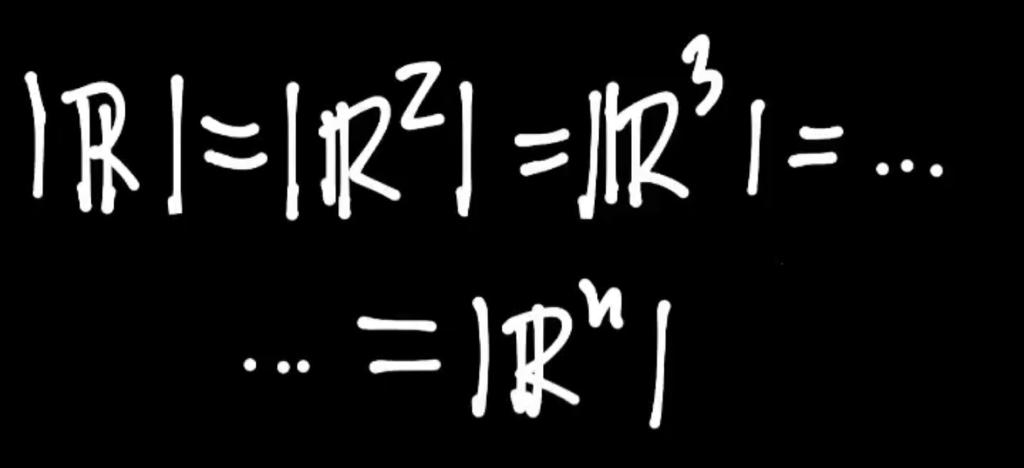
Vamos que el infinito del continuo R -o del intervalo (0,1)– es igual que el del plano R², el del espacio de tres dimensiones R³ o ¡el de un espacio de n dimensiones Rⁿ !

Y para que nos acabe de explotar la cabeza: Si se piensa nuestro universo como un espacio euclidiano de tres dimensiones R³, tal y como lo hacía el gran Newton, esto equivale a decir, nada más y nada menos, que hay los mismos puntos en todo el universo que en el intervalo (0,1).

Más allá de las matemáticas, la cuestión es qué se tapa con estas fantasías hechas en el rigor del matema, y qué suponía Cantor, y antes que él Spinoza, bajo la disciplina de estas formulaciones matemáticas sino, él lo llegó a decir, un Dios completo y omnipotente, un Otro sin falta, un infinito de los infinitos.

«La solución de los problemas que hasta ahora rondaban al infinito matemático es probablemente el mayor de los logros de los que nuestra época pueda enorgullecerse».

BERTRAND RUSSELL, EN 1910

ENM (2023)