Seguimos con los delirios de Cantor. Decimos bien, delirios, pues Cantor con sus pensamientos se salía del surco de los caminos trillados.

Ya mostramos en una entrada anterior que los cardinales de los números naturales N = {0,1, 2, 3, … } y de los números reales R siendo ambos infinitos, es decir, teniendo ambos conjuntos un número infinito de elementos, tenían un orden distinto, pues el infinito de R, al no poderse contar, era mayor que el de N. Esto lo escribíamos |N|<|R|.

También mostramos en otra entrada que

|N|<|R|=|R²|=|R³|=…=|Rⁿ|

No obstante esta circunstancia, Cantor puso en marcha lo que denominó la aritmética de los transfinitos que suponía conjuntos de infinitos mayores que el de los reales R.

Pero vamos hoy a por otro interrogante que se planteó el genio matemático de Georg Cantor y que fue fundamental para las matemáticas del siglo XX:

¿Existe un conjunto A tal que |N|<|A|<|R|?

Lo que nos estamos preguntando ahora es si existe otro conjunto A de infinitos elementos, pero con un orden intermedio, es decir, dicho de otra manera, nos preguntamos si existe un infinito mayor que el de los números naturales, pero menor que el de los números reales.

Cantor pensaba que no existía ese conjunto A, pero no pudo demostrarlo en vida. De aquí que quedara formulado como una mera hipótesis: «no existe un conjunto con un cardinal intermedio entre el cardinal del conjunto de los números naturales y el cardinal de los reales». Esta hipótesis, pendiente de demostrar, se denominó en el mundo de las matemáticas, justamente, La hipótesis del continuo.

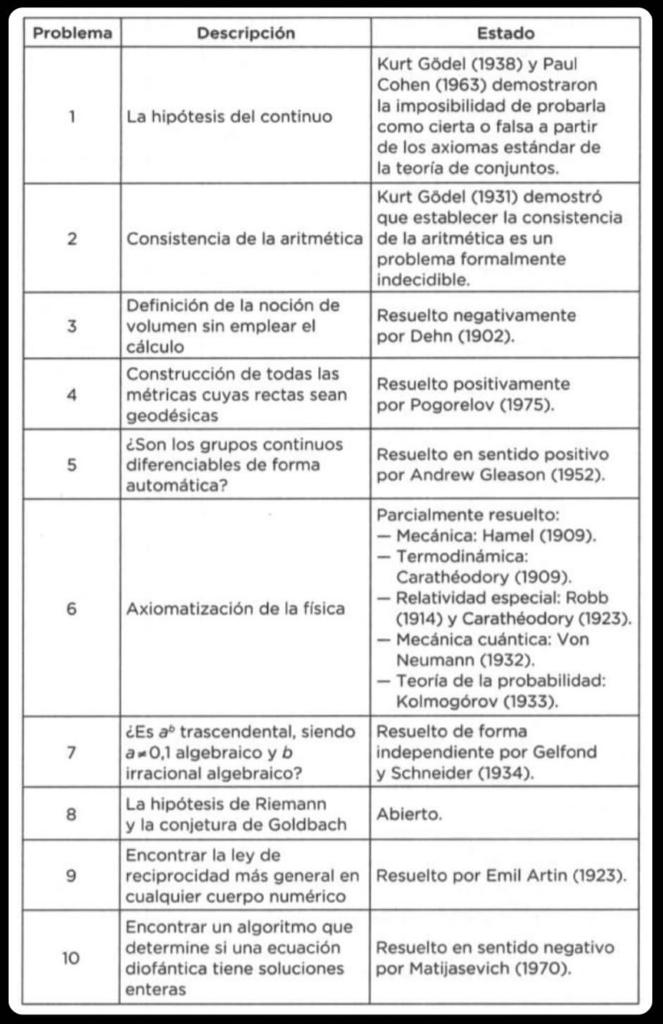
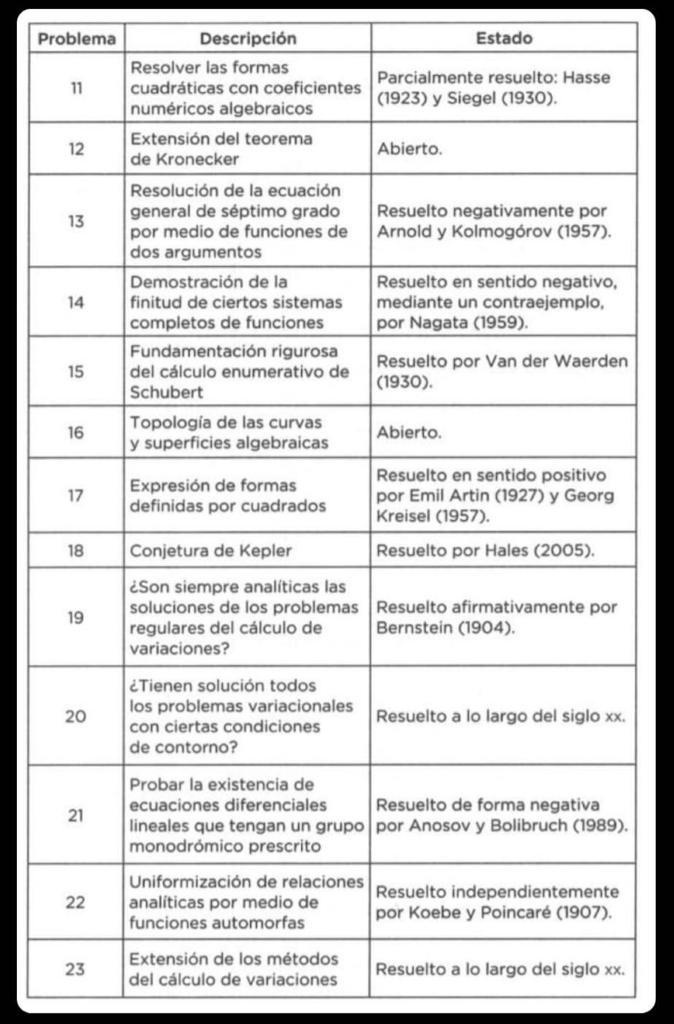
En 1900, otro gran matemático, David Hilbert, enumeró los 23 problemas de matemáticas más importantes para el siglo XX y el primero de la lista fue precisamente ¡ La hipótesis del continuo !

Como decíamos, Cantor pensaba que no existía ese infinito de orden intermedio entre el infinito de los naturales y el de los reales. Otros matemáticos, como por ejemplo el brillante Gödel, pensaban que esta hipótesis del continuo de Cantor era falsa y que sí existía ese conjunto A tal que |N|<|A|<|R|.

La cosa, por lo tanto, era:

¿La hipótesis de continuo de Cantor es verdadera o falsa?

El problema permaneció abierto hasta el año 1966 en que el matemático estadounidense Paul Cohen demostró que el problema no tenía solución, esto quiere decir, ¡atención!, no que la hipótesis sea falsa, sino que es un problema cuya solución es indecible, es un problema que no se puede decir a partir de los presupuestos axiomáticos de la teoría de conjuntos que los matemáticos daban por buena desde inicios del siglo pasado.

Esto es muy importante porque habitualmente se piensa que una proposición matemática o bien es verdadera o bien es falsa, y que, además, no hay una tercera opción. ¡Craso error! También hay problemas matemáticos irresolubles por indecibles.

La contribución de Paul Cohen, en un gesto matemático muy gödeliano, puso de manifiesto el agujero que hay en el centro mismo de toda axiomática que se toma por fundamento último de la matemática, en este caso este vacío fue identificado, via la hipótesis del continuo, en la Teoría de Conjuntos de Zermelo-Fraenkel, una axiomática que, como decíamos hace un momento, se consideraba como definitiva desde principios del siglo XX.

Está bien, muy bien, que los delirios matemáticos de Cantor desembocaran, casi cien años más tarde, en la conclusión de que siempre hay un indecible en el decir, que siempre hay un resto que el matema, la trama significante del formalismo matemático, no puede aprehender. A lo sumo, el matema podrá seguir dando vueltas entorno a ese punto ciego imposible, y con el trayecto de esos rodeos ir delimitando el vacío: ese hueco de lo indecible en el decir mismo.

«Nadie nos expulsará del paraíso que Cantor ha creado para nosotros.»
– David Hilbert 

ENM (2023)