Se ha escrito poco sobre Georg Cantor, y en especial, además, se ha escrito muy poco, casi nada, sobre el decir en acto de Cantor.  ¿Qué es lo que caracteriza este decir mismo? A saber, el ser un decir que se singulariza por su fidelidad a la letra, por su perseverancia obstinada en no esperar un sí o un no del Otro a la hora del despliegue de la lógica del significante matemático, del matema para ser exactos. El decir de Cantor se ciñe al rigor implacable de la matemática sin esperar la aprobación o la desaprobación de ese Otro que, en su tiempo, tenía como lugarteniente al matemático Kronecker, un representante de lo que el fantasma de la tradición venía dando por bueno, sabido y consabido en relación a los números y, muy particularmente, en relación al infinito. 

La historia es de sobras conocida: para Kronecker, como para toda la tradición desde Aristóteles llegando a Galileo e incluso a Kant, no hay más infinito que el infinito potencial, el infinito en acto es una ilusión, una ficción estéril. El argumento: puede suponerse un espacio o una cuenta 1, 2, 3… como potencialmente infinitos, pero a la que las consideramos como infinitudes actuales surgen contradicciones insalvables. Aristóteles, que pensaba en términos geométricos, dirá que si concebimos un todo espacial, éste habrá de estar incluido en el algún lugar, luego ya no será un todo. Galileo, punto de arranque de la física moderna, muy hábilmente verá que si consideramos los números naturales 1, 2, 3…  y los números pares 2, 4, 6… como un todo, en su infinitud en acto, llegamos a la paradoja de que, por un lado, siendo los pares un parte de todos los naturales debe haber una cantidad menor de los mismos, pero que, por otro lado, dado que puede establecerse una relación de uno a uno entre números naturales y números pares, hay una misma cantidad de unos y otros números. Dicho lo cual, el Otro de la tradición, el de la convención social, venía sellando bajo el semblante del sentido común la pertinencia del infinito potencial y la locura de considerar el infinito en acto.

La grandeza de Cantor consistió en que no se detuvo frente a estas dificultades. Cantor no se debía al Otro, su fidelidad era con respecto al matema, su decir mismo se sitúa al nivel de la letra; por ello, justamente, acabará siendo el artífice de la teoría de conjuntos y del álgebra tal y como la conocemos en la matemática contemporánea. Esta fidelidad al matema tendrá un gozne doble: primero, suspender lo imaginario de las concepciones que piensan el infinito en claves geométricas, físicas e incluso metafísicas, y segundo, consecuencia de lo anterior, un ceñirse al sinsentido de la letra, a lo que queda del significante cuando hacemos abstracción del significado, para pensar el infinito en clave de conjuntos y de manera estrictamente algebraica. Desde luego, la posición de Cantor tiene algo de loca por cuanto barraba el Otro, y no lo barraba indicando un agujero en el Otro para, seguidamente, persistir en él -un modo de barramiento típicamente neurótico, una separación o Entbindung al decir de Freud-, sino que suspendía ese Otro como tal, avanzaba de manera delirante negándole sus galones y existencia misma para ceñirse, como decimos, al goce de la letra. Un verdadero pasaje al acto, en suma.

Primera negación en el decir de Cantor: reconocimiento de la realidad del infinito en acto. El infinito es una cantidad bien determinada, como la de cualquier otro número. Dicho aún de otra manera aún más esclarecedora: el infinito es un número. Si nos atenemos a los números naturales 1, 2, 3… , hay un número más que culmina esta cadena: ω, este es el primer infinito en acto o, como él lo bautizará, el primer número transfinito. 

1, 2, 3, …, ω

Este gesto decisivo de Cantor puede parecer injustificado, pues ω no puede obtenerse en modo alguno a partir de la operación de suma con el resto de números naturales, pero el mismísimo genio de Gödel ya señaló muy pertinentemente que ocurría exactamente lo mismo con el número 2 y ¡nadie se escandalizó! ¿Cómo? ¿No tenemos que 1+1=2? Efectivamente, pero de lo que aquí se trata es de obtener un número sin tenerlo por anticipado, y esta suma, 1+1, como ya se habrá percatado el lector avispado, presupone el 2, pues hay en ella un número de términos que se adicionan igual a 2. No ocurre lo mismo a partir del 2, pues 3=2+1, 4=3+1, etc.

Lo que es sumamente interesante es que este reconocimiento de los títulos de ω, argumentará Cantor, no es distinguible del que realizamos cuando, por ejemplo, pensamos un triángulo equilátero con catetos de magnitud 1 o cuando pensamos un círculo cualquiera, pues en ambos casos se sostiene la realidad de dos números irracionales, esto es, de dos números con infinitos decimales no periódicos en acto: 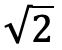 y  .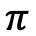

Segunda negación en el decir de Cantor: No hay un infinito, sino infinitos infinitos. Para alcanzar esto sólo hay que extender lo que presuponemos para los números naturales, a saber, que son ordinales, esto es, que 0 es un ordinal y que, dado que cualquier número natural es igualmente ordinal, basta sumar 1 para tener un sucesor que será también un ordinal. Cantor sigue con esta lógica a partir de ω y con ello obtiene nada más y nada menos que la cadena números transfinitos:

ω, ω+1, ω+2, …, ω+ω=2ω, 2ω+1, 2ω+2, …, ω², …, ,…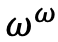

La deducción de Cantor, como venimos señalando, no responde a argumentos imaginarios de orden espacial, físico o metafísico, sino que se ajusta de manera rigurosa al decir mismo de la matemática, a su propia lógica algebraica. Este proceder loco que suspende el Otro es, sin duda, el síntoma de Cantor, un síntoma que se proyectará en toda la matemática posterior a él, aunque los matemáticos aún hoy no sean muy conscientes de ello.

Tercera negación: estos infinitos actuales o números transfinitos pueden tener diferente magnitud. Hay unos infinitos en acto mayores que otros infinitos en acto. Cantor pasa a considerar aquí la cardinalidad, esto es, el número de elementos de los conjuntos asociados a estos infinitos. El caso consabido que pone de manifiesto esta consecuencia última es la cardinalidad diferente que tienen los números naturales de una parte y los números reales de otra parte, cosa que nuestro matemático elucidó demostrando, mediante su método de la diagonalización, que los reales no son numerables. Aquí es donde Cantor, para denotar la cadena de cardinalidades, introdujo su celebérrima notación que usa la primera letra del alfabeto hebreo aleph.

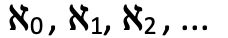
Dicho sea de paso, la hipótesis del continuo que Cantor postuló y no pudo demostrar, consistía en que 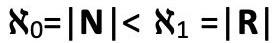. Hoy sabemos gracias Kurt Gödel y Paul Cohen que dicha hipótesis era indemostrable por indecible, es decir, que no podía demostrarse que el segundo cardinal  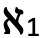fuera el cardinal de los números reales |R|. Es este impasse en la formalización matemática, la imposibilidad para escribir lo indecible que habita en el decir matemático mismo, lo que, según Lacan, permite un acceso a lo real. En cualquier caso, esto no impidió que Cantor pusiera en marcha toda una aritmética de los números transfinitos sorprendente que, entre otras muchas cosas, mostraba que  

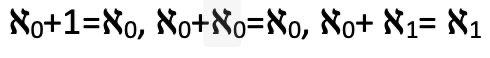
o que

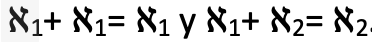
Y cuarta negación: Cantor postula que hay un infinito absoluto 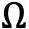, para seguidamente decir que los infinitos actuales o números transfinitos de los que él se ocupa con la matemática no son absolutos, pues estos son dependientes, susceptibles de aumento y perfeccionamiento (ω, ω+1, ω+2…), no así el infinito absoluto, el cual es suma perfección, independiente y extramundano, además de inaccesible para nosotros. En suma, este infinito absoluto es Dios. La apertura de esta brecha entre infinitos en acto e infinito absoluto establecida por Cantor suele interpretarse como un gesto de alienación en el Otro, como una denegación para evitar el sentimiento de culpa que le acompañaba al tratar con un infinito actual que no pocos adversarios suyos identificaban con lo divino. Él ocupándose de los números transfinitos hacía matemática, lo absoluto era cosa de teólogos. No obstante, quizá sea más acertado, aunque también más arriesgado, leer el paso al infinito absoluto realizado por Cantor a partir de su síntoma, como una negación más que sustenta su pasaje al acto, su suspensión del Otro. Bajo esta perspectiva, la postulación del infinito absoluto debe interpretarse como una consecuencia última del lenguaje, lo que a la postre, a contracorriente de la consabida fe de Cantor, sería una declaración ateológica. Es el lenguaje mismo, como pone en evidencia la deducción de la existencia de  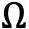a partir del lenguaje matemático de Cantor, el que induce a una disposición religiosa, así como a la suposición de un Dios.

Tenemos, pues, cuatro negaciones en acto del Otro que se sustentan en el rigor del matema, en el goce de la letra. Y es que, justamente, esta adhesión y fidelidad de Cantor al matema, este silenciamiento de la enunciación y sus fantasmas para ceñirse al literal de los enunciados matemáticos mismos, era estrictamente correlativa de su síntoma, de su elección loca, delirante, por desligarse del Otro, de su pasaje al acto. 

«La esencia de las matemáticas es la libertad» 
– Georg Cantor 

ENM (2023)