En 1903 Poincaré formuló la famosa e importante conjetura que, a título póstumo, lleva su nombre. Esta conjetura asegura que en una esfera cuatridimensional todo lazo homeomorfo (deformable) a un círculo puede transformarse en un punto.

Demos, cosa no muy del gusto de los matemáticos, una imagen intuitiva de qué significa esto:

Una 1-esfera es un círculo, una 2-esfera una especie de pelota, una 3-esfera puede imaginarse como una 2-esfera que se expande y se contrae, etc. y así sucesivamente pueden pensarse esferas de n dimensiones, hasta alcanzar n-esferas.

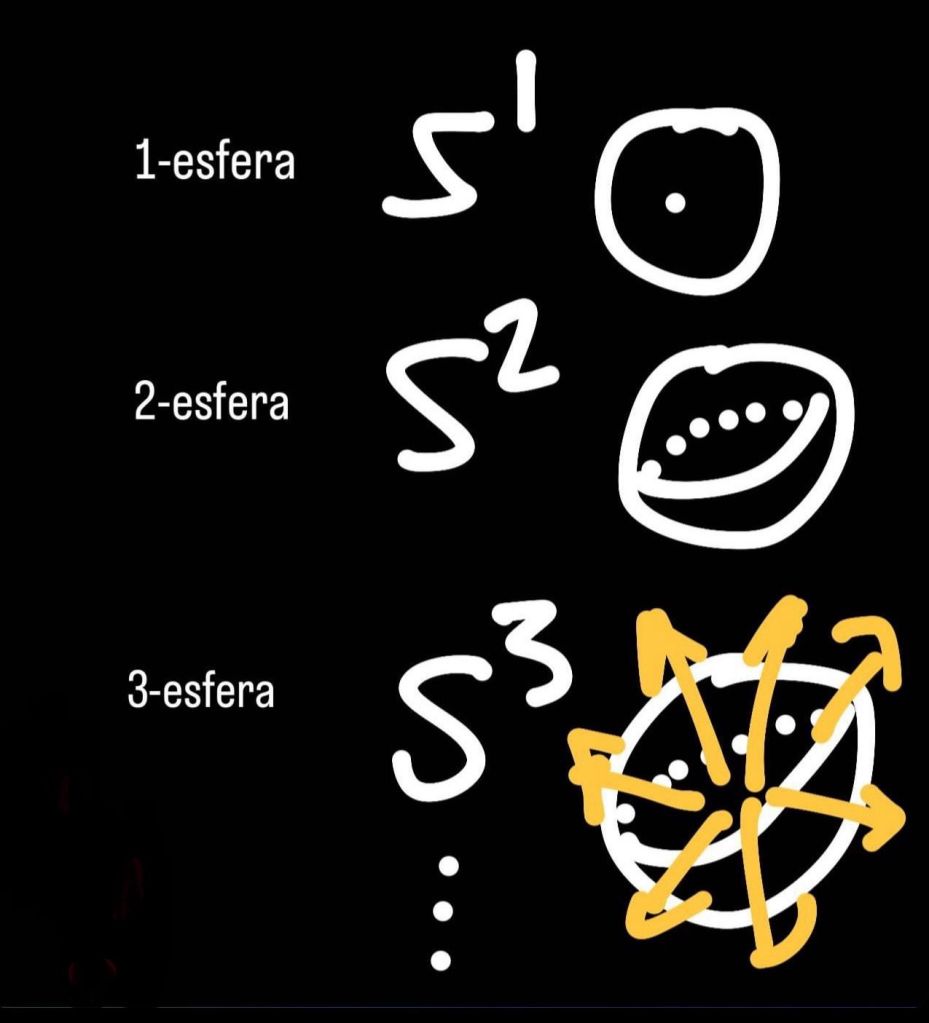
A partir de una 2-esfera, como decimos, podemos llegar a imaginarnos el problema para la 3-esfera, es decir, la Conjetura de Poincaré:

Mediante esta representación podemos ver intuitivamente cómo los lazos homeomorfos a un círculo se pueden ir transformando paulatinamente hasta alcanzar un punto. Pues bien, la Conjetura de Poincaré supone afirmar esto mismo para una 3-esfera, esa esfera que, como decimos, podemos imaginar como la esfera común (una pelota), pero en expansión y contracción.

Como señalábamos hace un momento, la Conjetura de Poincaré fue enunciada en 1904 por el gran matemático Henri Poincaré. De formulación relativamente sencilla, el problema fue considerado, desde un buen inicio y hasta hace muy poco tiempo, uno de los problemas matemáticos más difíciles de resolver.

Y en eso llegó el matemático ruso Grigori Perelman, un verdadero personaje considerado como una de las personas más inteligentes del planeta y, en el año 2006, 100 años más tarde de la primera formulación dada por Poincaré, demostró la conjetura. Se cuenta que cuando Perelman estaba a punto de finalizar su demostración pasaba las horas en un ensimismamiento delirante, con una mueca sonriente absurda y con comportamientos sumamente extraños que tenían en vilo, muy preocupada, a su adorada madre. Estaba absorto, poseído por los objetos matemáticos. Platón, sin duda, hubiera afirmado que Grigori estaba tomado por el daimon socrático.

Lo interesante, además, es que, tras demostrar la importante conjetura, Grigori Perelman recibió la Medalla Fields (el nobel de las matemáticas) a la cual renunció arguyendo que no lo iban a convertir en un mono de feria. Poco después, también le otorgaron el premio de 1 millón de dólares en que estaba valorada la demostración de la conjetura, también renunció al dinero asegurando que había hecho su trabajo y que lo realmente valioso era la demostración de la conjetura. Estos gestos de Perelman constituyen verdaderos pasajes al acto, constituyen una negativa última a las demandas por las cuáles el gran Otro te convoca.

Actualmente Perelman vive con su madre de manera humilde, como un asceta, en un barrio popular de San Petesburgo. Dejó el Instituto de Matemática Steklov, declinó formar parte de la prestigiosa Academia de Ciencias Rusas y se especula gratuitamente sobre si continúa o no haciendo matemáticas. Sólo ofreció una única y rara entrevista en 2010 en el periódico Pravda en la que aseguraba nada menos que él «puede controlar el universo». Hay quienes ponen en duda si realmente se produjo esta entrevista. Dicen que la última vez que Grigori fue físicamente visto fue en el Metro de San Petersburgo en 2008.

En cualquier caso, Perelman lleva una vida retirada, prácticamente de anacoreta. Perelman, en definitiva, es un suicidado de la sociedad, ese título con el que Antonin Artaud bautizara a Van Gogh, otro grande, pero no de la matemática, sino de la pintura.

ENM (2023)