Es común pensar que Leibniz fue un pensador de la necesidad, como Spinoza, cuando en realidad fue un pensador de lo posible y, por lo tanto, de la contingencia. Si en Spinoza cualquier cosa es la manifestación necesaria de la esencia de Dios, esto es, de la totalidad de lo real (Deus sive natura) y sus leyes (more geometrico), en Leibniz cualquier cosa es o podría no haber sido, ergo es contingente, pero si efectivamente es, como decimos, no parece seguirse por necesidad, sino más bien por ser una posibilidad realizada, actualizada como consecuencia de una pretérita y libre elección divina. Por consiguiente, son múltiples las realidades que podrían y pueden llegar a ser, hay muchos mundos posibles, pero al final uno sólo se realiza, el mejor de los mundos posibles, los otros quedarán ahí, sin realizar, como mundos virtuales, como mundos que pudieron haber llegado a ser, pero no fueron. Desde luego, siempre puede argüirse que, siguiendo el modo de argumentar de Leibniz, esa elección divina no es arbitraria sino racional, luego podemos objetar a nuestro filósofo que la de Dios no es una verdadera elección, que no hay libertad, pues siendo un ser racional no le quedaba otra que elegir lo que eligió, a saber, lo más racional, el mejor de los mundos posibles y no otro. A lo que, en un círculo vicioso, siempre se podrá replicar que sí, que es o, más bien, fue una elección racional, pero que no por ello, al fin y al cabo, deja de ser una elección. Subyace aquí la famosa polémica con Descartes, el cual pensaba que Dios, pudiéndolo todo, quiso que 2+2 fueran 4, lo racional, pero podría haber hecho que no fuera así y haber establecido que 2+2 fueran 5, a lo que Leibniz respondía que de eso nada, que Dios no podía no elegir que 2+2 fueran 4, porque pertenece a la esencia misma de Dios el ser racional. Leibniz, aun siendo un pensador de la contingencia y la libertad, no puede evitar que, en la medida en que invoca a un Dios esencialmente racional, se le cuele la necesidad por la puerta de atrás. En el juego de estos entresijos conceptuales está gran parte del mérito y las contradicciones de Leibniz: el filósofo quiere pensar la libertad, la contingencia, pero no está dispuesto a prescindir de un Dios racional que sea garante de un mundo armónico, del mejor de los mundos posibles. 

En todo lo caso, lo que cabe destacar ahora es que, tras esa manera de pensar de Leibniz, se convoca de manera incuestionable lo posible, el universo de la posibilidad, esos mundos posibles, virtuales, lo que a la postre nos permite traer a colación una idea clave para la historia de las matemáticas y la invención del cálculo que el polímata alemán ideó. Nos referimos a la idea de diferencial dx. ¿Qué es un diferencial dx? Es una cantidad infinitamente pequeña diferente de cero, la más pequeña variación o diferencia de una cantidad considerada, x + dx por seguir con el ejemplo, y es tan pequeña que no es asignable, es una virtualidad a la que, consiguientemente, no cabe atribuirle número ninguno, pues, como decimos, es más pequeña que cualquier cantidad dada o dable. La paradoja salta a la vista rápidamente: se afirma, a un tiempo, que un dx es una cantidad, una diferencia, y que, no obstante, puesto que es una cantidad infinitamente pequeña, no podemos asignarle cantidad dada ninguna. Estamos ante las paradojas de lo infinito. Pero no nos adelantemos por el momento, sigamos con Leibniz. Ahora bien, lo asombroso es que puede darse el caso en que, tomados dos diferenciales dx y dy, la proporción entre ambos, dx/dy, sea una cantidad asignable perfectamente expresable. Leibniz ponía de manifiesto esta circunstancia a través de triángulos semejantes:

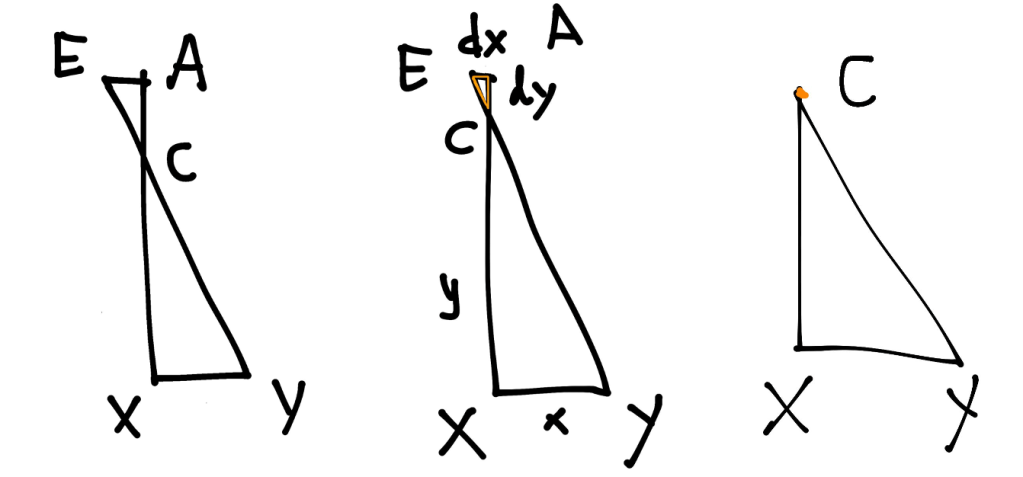
Dado que los triángulos AEC y XYC son semejantes tenemos que AE/AC=XC/XY=a donde a es una cantidad determinada. Ahora, si notamos XY=x y XC=y, y contemplamos la posibilidad de hacer del triángulo AEC una virtualidad infinitamente pequeña, esto es, si llevamos AE y AC al estatuto de diferenciales, AE=dx y AC=dy, entonces, ¡oh milagro!, tenemos que

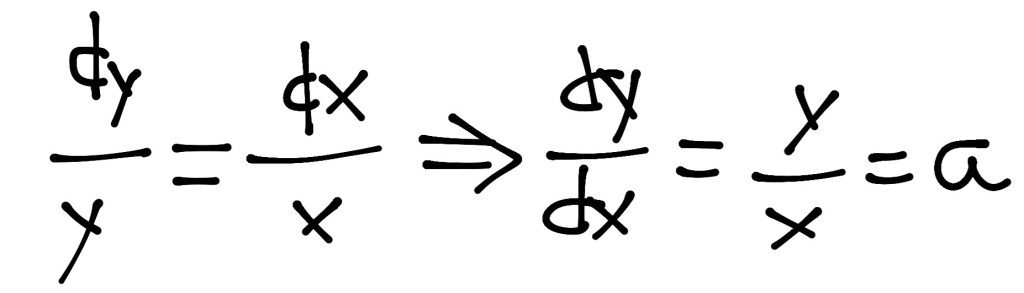
Inspirado en el Traité des sinus du quart de Cercle de Pascal, Leibniz tuvo la temprana iluminación de utilizar estos triángulos virtuales para obtener lo que hoy denominamos «derivada», a saber, la pendiente de la recta tangente en un punto de una curva cualquiera.

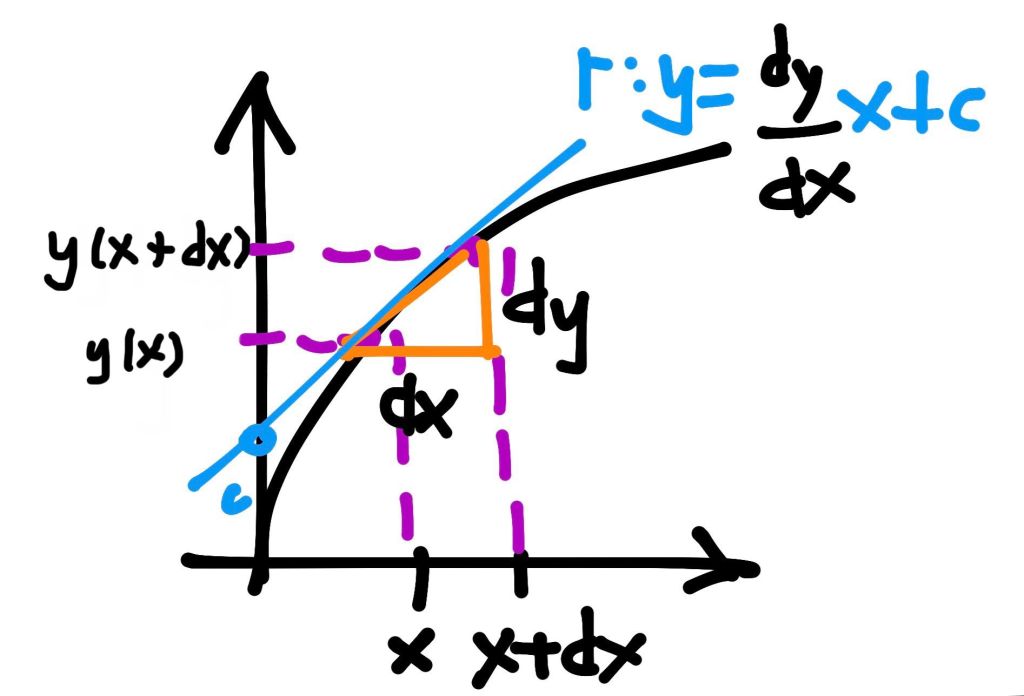
A partir de aquí el cálculo de las derivadas era relativamente sencillo. Bastaba considerar la siguiente fórmula:

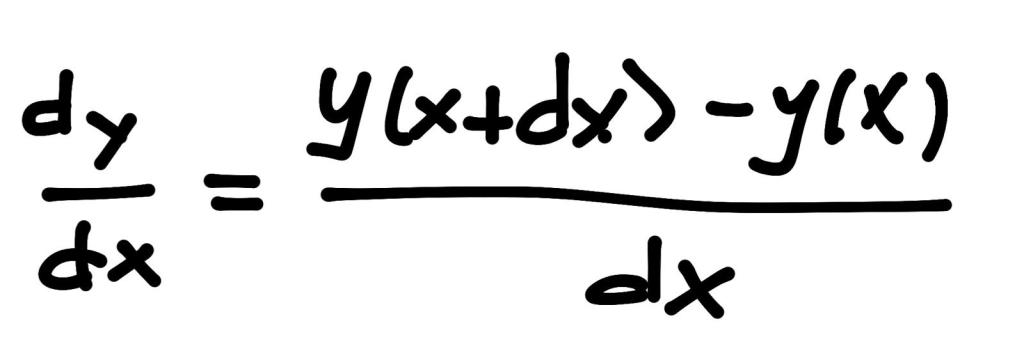
Veamos algunos ejemplos sencillos. Empecemos por la derivada de una constante:

Derivada de una recta cualquiera:

Derivada de una parábola:

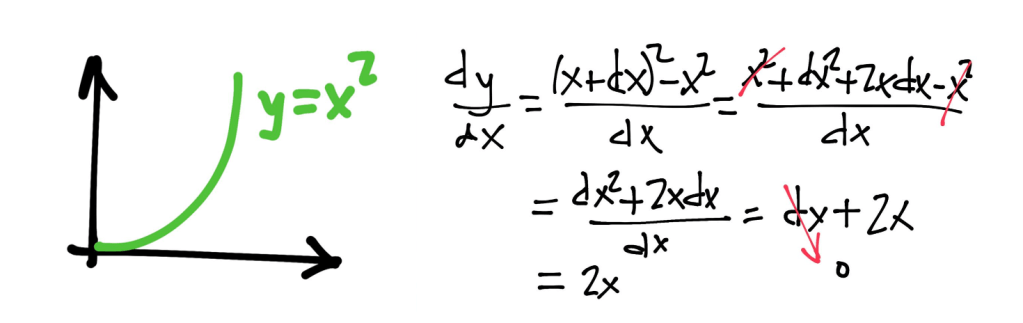
El caso de la parábola es especialmente relevante porque apunta a una dificultad matemática que trajo de cabeza a Leibniz, también a Newton con sus célebres fluxiones. Tal y como hemos visto, el dx era caracterizado por Leibniz como una cantidad infinitamente pequeña, evanescente, como una cantidad más pequeña que cualquier cantidad dada o dable pero diferente de cero y, sin embargo, como vemos, en el paso final para obtener el cálculo de la derivada tenía que considerar dx como igual a cero. La pregunta que rápidamente vino a colación fue: ¿cuál es el verdadero estatuto de estos diferenciales dx? Leibniz se topaba aquí con una roca que se resistía al matema, a una formalización consistente, la propia formalización matemática con la que él obtenía las derivadas y fundaba el cálculo infinitesimal no adolecía de contradicciones. Es más, cuando nuestro filósofo jugaba a imaginar dichos diferenciales en claves metafísicas llegaba igualmente a conclusiones inverosímiles. Sin ir más lejos, por citar un solo ejemplo, asumiendo la existencia de los diferenciales, y pensando lo grande y lo pequeño como una cuestión de escala, podía pensarse el diferencial dx como una línea terminable, cosa que suponía considerar que era un algo que, aunque infinito, esto es, infinitamente pequeño, tenía paradójicamente un inicio y un fin. Es más, este diferencial, por cuanto era infinito, infinitamente pequeño, entrañaba una eternidad que, considerada bajo nuestra escala, pensaba Leibniz, no era sino una eternidad evanescente, efímera, un mero suspiro. Consecuentemente, si se daba estatuto de realidad al diferencial dx, no había una sola eternidad, sino diferentes eternidades, cosa que no podía sino perturbar a Leibniz.

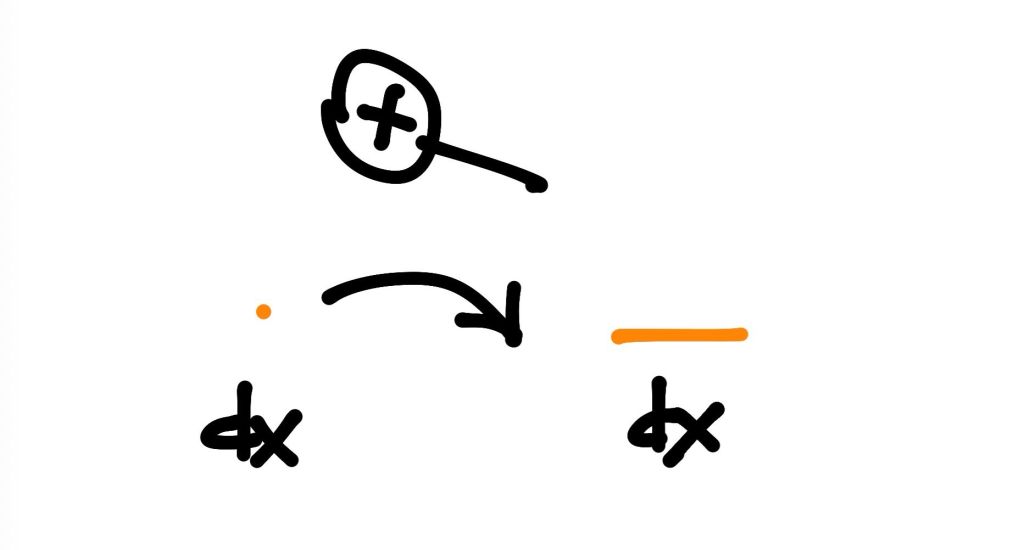
Tras no pocas dudas y algunos rodeos, hacia el final de su vida, la posición de Leibniz no dejó lugar a equívocos: los diferenciales dx son ficciones útiles y el procedimiento algorítmico que los pone en funcionamiento no pasa de ser una mera heurística, un lenguaje útil que permite producir eso que acabó dándose en llamar «cálculo diferencial». Así, podemos encontrar en un texto escrito en septiembre de 1714, dos meses antes de su muerte, lo siguiente:

«En cuanto al cálculo de los infinitesimales (..) cuando (nuestros amigos) se disputaban en Francia (..), les manifesté que yo no creía que hubiera magnitudes verdaderamente infinitas ni verdaderamente infinitesimales: que sólo eran ficciones, pero ficciones útiles para abreviar y hablar universalmente (..). Pero como el señor Marqués de L’Hôpital creía que por ello yo traicionaba la causa, me rogaron que no dijera nada, aparte de lo que había dicho en un lugar de las Actas de Leipzig; con placer accedí a su ruego.»

El texto de Leibniz tiene todo el aire de lo que Freud catalogará, con el paso del tiempo, como denegación: no hay, no hay… ergo… estás diciendo que lo hay. La cuestión, en todo caso, es: ¿ante qué retrocedía Leibniz? El fragmento arriba nos da la respuesta de una forma clara, sólo basta leerlo a la letra: se retrocede ante el infinito. Leibniz afirma que no hay verdaderamente cantidad infinitamente grande o infinitamente pequeña, dicho de otro modo, sostiene que no hay infinito en acto. Lo que Leibniz se resiste a aceptar, por tanto, es la actualidad de un posible, la actualidad de lo que para él tiene, y no puede dejar de tener, un estatuto virtual. Digámoslo ya, lo decisivo es que Leibniz, aun habiendo tenido bajo sus pies un camino que recorrer, un camino que ha sido gestado por su propia formalización matemática del cálculo mediante diferenciales, se detiene, renuncia a llevar hasta las últimas consecuencias un análisis infinito, y se detiene ahí donde Cantor, mucho después, dará el paso justamente opuesto, a saber, permanecer en el delirio de una fidelidad al matema que le permitirá acabar formalizando lo real de un infinito actual. Y es que Leibniz era un tipo de orden, tanto que, a pesar de ser considerado el paradigma de filósofo racionalista, no fue lo suficientemente racionalista como para lanzarse a la aventura loca de la formalización algebraica del infinito y de un análisis infinito. Su fidelidad a lo racional y al matema terminaban ahí donde hubiera tenido que, como hizo Cantor, hacer frente a las dificultades sumas que conllevan el pasaje al acto: tachar el Autre, agujerearlo, negarle su autoridad, lanzarse al abismo de un ceñirse a lo real del matema sin esperar un sí o un no de ese Autre de la convención que, desde Aristóteles, imaginaba lo infinito en claves geométricas, como algo potencial, al tiempo que motejaba de absoluto despropósito toda tentativa de pensar el infinito en acto. Lo señalábamos poco más arriba, ese Dios racional que convoca Leibniz, aunque traiga a escena la contingencia en una supuesta decisión, no deja de ser el síntoma de un Leibniz que tiene la necesidad de encontrar unos u otros subrogados que hicieran las veces de garante, diversos semblantes de un Autre completo que está llamado a encarnar una totalidad por completo legislada, armónica y previsible, como en Descartes y Spinoza. Es de esos subrogados de Dios de los que no podían prescindir Descartes, Spinoza o Leibniz. Sí prescindió de ellos Cantor, aun al precio de una terrible crisis existencial y religiosa que lo llevó a la locura, el internamiento en un manicomio y su muerte final.

Lo que no deja de ser igualmente sintomático, además de un tanto escandaloso, es que la historia, extendiendo la sombra de temor del viejo Leibniz, alicatara por más de 250 años la idea de que el cálculo basado en diferenciales no pasaba de ser una heurística. De hecho, siguiendo esta estela, el cálculo halló una formalización satisfactoria a inicios del siglo XIX que eludía los diferenciales dx y que partía de la noción de límite desarrollada por los matemáticos Cauchy y Weierstrass, una noción que, como cualquier matemático sabe -un límite es acercarse a un punto (el límite) tanto como se quiera sin por ello alcanzarlo-, descansa en un infinito potencial y, por tanto, también repudia el infinito actual. De hecho, este es el cálculo que aún hoy se enseña en las facultades de matemáticas de las universidades del mundo entero. Y ello, a pesar de que en el año 1966 un ingenioso matemático, llamado Abraham Robinson, consiguiera nada más y nada menos que elaborar una teoría matemática rigurosa, la llamó «Análisis No Estándar», que formalizaba el cálculo, prescindiendo de la noción de límite, y extendiendo los números reales estándares (los de toda la vida) con los infinitos -los números infinitamente grandes- y los infinitesimales -los números infinitamente pequeños- considerados como actuales, esto es, siguiendo la inspiración de Cantor, considerando cada infinito y cada infinitesimal como un número más. Además, Robinson consiguió que dicha extensión de los números reales habituales con infinitos e infinitesimales tuviera una estructura algebraica con las mismas propiedades que los números reales, es decir, que fuera lo que los matemáticos denominan «cuerpo». Los elementos de esta extensión son los números hiperreales, y el cuerpo fue notado como R*.

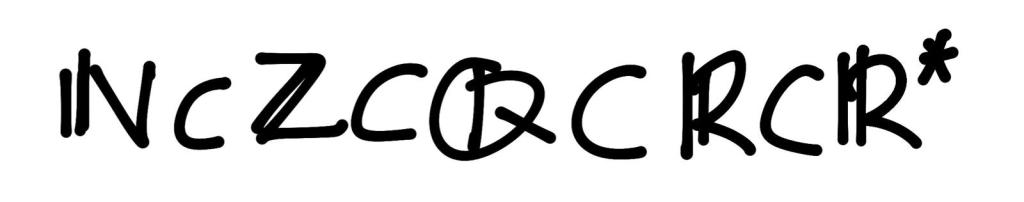
Los hiperreales, pues, incluyen los siguientes tipos de números:

• Los números x de R* tales que para cualquier n natural se tenga |x|<1/n. Es decir, un número x que cumpla este requisito es más pequeño que cualquier número real dado o dable. Es, en suma, un infinitesimal o un infinito pequeño. Los denotaremos con la letra 𝜀. No se le escape al lector que estos 𝜀 son los dx de Leibniz.
• Los números x de R* tales que para cualquier n natural se tenga que |x|>n. Es decir, un número x que cumpla esta condición es más grande que cualquier número dado o dable. Estamos ante los infinitos o infinitos grandes. Los denotaremos con la letra w.
• Los números x de R* que son los reales de toda la vida, esto es, que pertenecen a R. Son los números reales estándares.
• Luego, para finalizar, están los números x de R* que son la suma de un número real estándar r perteneciente a R y un infinitesimal 𝜀, es decir, x=r+𝜀. 

Ahora bien, volvamos a lo que nos interesa, a saber, el cálculo. ¿Qué ocurre en el universo de los hiperreales con las derivadas y las inconsistencias aparejadas a los dx con que se encontraba Leibniz? Volvamos a la parábola:

Robinson soluciona la incoherencia de Leibniz de igualar a cero el diferencial dx de una manera sencilla y elegante. Dado que la derivada debe ser un número real R y, como vemos, hemos obtenido un número hiperreal que incluye un infinitesimal dx+2x, bastará quedarse con la parte real estándar de dicho número hiperreal, esto es, con 2x. Robinson lo denota así:

Llegados a este punto, lo que es sumamente paradójico es plantearse, con un criterio a lo Leibniz, como pudo ser que este análisis no estándar, o el cálculo basado en los infinitesimales, un análisis infinito, permaneciera en un estado virtual, como posibilidad, por más de dos siglos y que, por el contrario, se actualizase la posibilidad de un análisis que, basándose en la idea de límite, siguió siendo refractario a los infinitos actuales. Una respuesta muy de Leibniz sería aseverar que la bifurcación entre análisis estándar y no estándar, entre un cálculo de los límites y uno de los diferenciales, y el hecho histórico de que el primero se actualizase, pasase a ser una realidad, y el segundo quedase en un estado virtual, como simple posibilidad, fue una contingencia, una contingencia necesaria que sólo entiende y compete a Dios. Únicamente Dios puede entender el hecho consumado de que todo transcurriera tal cual transcurrió y que ello condujera al mejor de los mundos posibles, pues sólo la omnisciencia divina podía tomar una decisión primigenia y racional que, contemplando por adelantado todos los posibles, incluida la encrucijada de Leibniz, tuviese la certeza de que no había razones suficientes como para que el polímata fuera consecuente, y sí las hubiere para que fuera del todo inconsecuente. Un completo delirio, en suma, pero un delirio que, no obstante, nos lleva a lo que aún hoy puede ser interesante: adentrarnos en toda esta lógica del pensamiento de Leibniz pero haciendo el vacío de Dios, aseverando que ese Autre no existe, prescindiendo de ese supuesto garante de la decisión más racional que nos asegura el mejor de los mundos posibles. Es así como podemos atisbar un pensamiento salvaje que nos arroja a la locura de pensar la contingencia al desnudo, en su radicalidad más cruda, sin una necesidad  que venga a salvarnos a última hora. Sin Dios pero con Leibniz, ya no se trata de pensar la necesidad de lo contingente, ya no es cuestión de poner un Dios que explique las razones suficientes de lo que se nos presenta como contingente sino que, por el contrario, de lo que se trata es de entender la contingencia de la necesidad, que nuestro mundo, sus razones y racionalidad, el análisis estándar, son un hecho contingente consumado envuelto de posibilidades no realizadas, un cálculo de los infinitesimales o un análisis infinito, y que el mundo por venir, con sus razones y racionalidad, con sus productos materiales y espirituales históricos que vendrán, será un hecho contingente por consumar sobre la base de posibles que podrán (o no) realizarse…

ENM (2025)