El problema de la braquistócrona, a saber, el de encontrar la curva de más rápido descenso, fue expuesto por Johann Bernoulli en 1696 en los siguientes términos: «Dados dos puntos A y B, en un plano vertical, hallar la curva a lo largo de la cual un punto material soltado en el punto A llega al punto B en un tiempo mínimo, suponiendo que no hay resistencia».

Newton, Leibniz, Jakob Bernoulli, que era el hermano mayor de Johann, llegaron por diferentes vías a una posible solución del problema, a saber: la conclusión, en absoluto inestimable, de que la cicloide cumplía con el requisito de la braquistócrona. Una de las respuestas al problema de la braquistócrona no era, pues, una de esas estupideces que dicta el sentido común, es decir, no era como suele creerse la recta. Ahora bien, ¿qué es la cicloide? La cicloide es la curva que tiene por traza la trayectoria de un punto situado en la frontera de un disco que rueda sin deslizarse a lo largo de una recta.

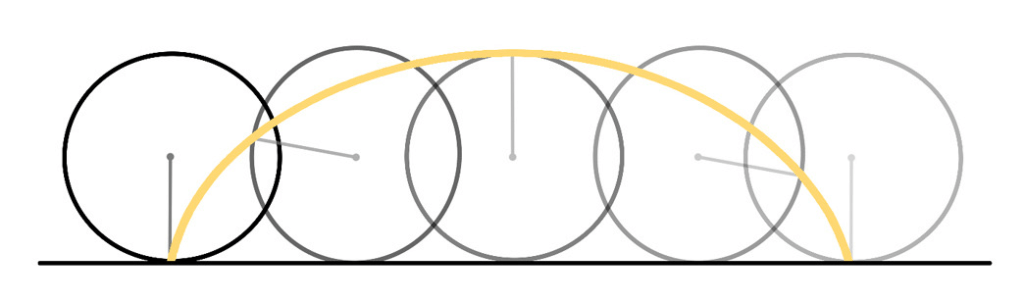
Lo que es decisivo es percatarse aquí de que, con lo avanzado por Newton, Leibniz y los Bernoulli, no podía descartarse que hubiera otras curvas cuyas trayectorias cumplieran el requisito de la braquistócrona. Para decirlo con Leibniz, el universo de lo posible o, mejor aún, la virtualidad misma que envolvía el problema de la braquistócrona estaba dada por una multiplicidad de curvas y la cicloide era una actualización de esa virtualidad, una actualización que no podía afirmarse por el momento como única. Es más, siempre podía verse con Leibniz que era un designio divino que la cicloide fuera la braquistócrona, dicho de otra manera, el posible que actualizaba la braquistócrona era la cicloide porque así era nuestro mundo, el mejor de los posibles, que eligió Dios con su infinita sabiduría.

Hubo que esperar hasta Leonhard Euler (1707-1783) para tener una demostración rigurosa de que la cicloide era la braquistócrona. El problema fue expuesto por Euler en su primera gran obra Methodus inveniendi lineas curvas maximi minimive proprietate gaudentes, sive solutio problematis isoperimetrici latissimo sensu accepti (1744). 

Volvamos por un momento a los hermanos Bernoulli. Johann llegó a la solución posible del problema inspirándose en una noción que Fermat presuponía en un trabajo acerca de la ley de refracción, la llamada Ley de Snell-Descartes. Esta noción afirmaba que la naturaleza opera por aquellos caminos que son más rápidos. No obstante esta circunstancia, fue su hermano Jakob el que abordó el problema aportando una propiedad esencial de la curva que minimiza el tiempo de descenso. La propiedad era la siguiente:

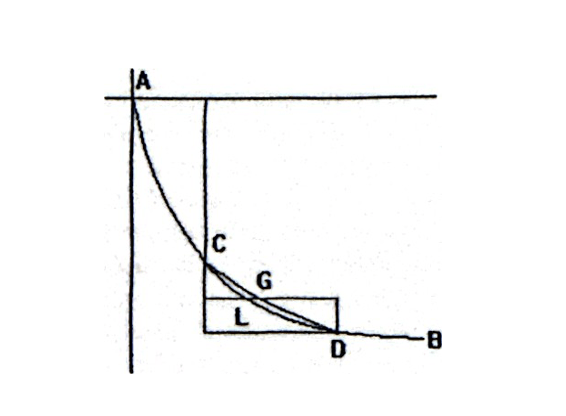
Si la curva ACGDB es la braquistócrona, con C y D infinitamente juntos, entonces la curva ACLDB, con L y G infinitamente juntos, también es braquistócrona. Es decir, que si ACGDB minimiza el tiempo de descenso también lo hace la curva ACLDB. Esta variación infinitesinal de la curva es una modulación continua de la misma que no altera su naturaleza, esto es, su carácter minimizador.

Esta propiedad tenía un carácter mucho más general de lo que el propio Jakob pensó, pues no sólo formaba parte de la naturaleza de la braquistócrona, sino de todas las curvas que maximizan o minimizan una determinada magnitud. Fue precisamente Euler quien cayó en la cuenta de ese hecho y el que lo usó para dar con una demostración rigurosa en su Methodus, una demostración que, como vamos a ver, no estará exenta de consecuencias filosóficas. 

Síntesis del método de Euler

El problema que se propone solucionar Euler es el de hallar una línea curva que tenga alguna propiedad de máximo o mínimo. Esa propiedad puede ser unir dos puntos sobre la esfera con distancia mínima, o hallar la curva que genera una superficie de revolución de volumen mínimo, etc.

Vamos a restringirnos a aquellas curvas que están referidas a una misma abscisa, intervalo, AZ. Notaremos por x la abscisa, y por y la ordenada. Convendremos, además, que d²x = ddx = 0. Notaremos también dy=pdx, dp=qdx, dq = rdx, … de donde se sigue que ddy=dpdx=qdx², dy=rdx³, …

Atención ahora a la fenomenal idea de Euler: Querer encontrar la curva que maximiza o minimiza una determinada magnitud (sea, por ejemplo, su longitud, o el área que encierra sobre la abscisa, etc.) es equivalente a dar con la curva que maximiza o minimiza una fórmula (funcional, operador) que al aplicarle las curvas da precisamente esa magnitud. 

Pongamos un ejemplo: Sea y una curva cualquiera referida a la abscisa AZ y sea W(y) = «la longitud de y», entonces hallar la curva más corta entre dos puntos puntos aA y zZ, será lo mismo, obviamente, que encontrar la curva y que minimiza W.

Euler lo expresaba de la siguiente manera: «en cualquier problema, la fórmula de máximo o mínimo será para nosotros aquella magnitud que en la curva que se quiere obtener deba alcanzar el valor máximo o mínimo».

La fórmula-magnitud deberá depender de la abscisa y de cada curva de manera particular. Es decir, y permitiéndome el uso de una notación ajena al Methodus, que W = W (x, y, p, q, …). Seguidamente, como el mismo Euler, pasamos a explicitar cómo es esa fórmula W. Haciendo camino llegaremos a la conclusión de que es de la forma ∫Ldx donde L = L (x, y, p, …), con cada y, p, q, … dependiendo a su vez de x, y además, ∫Ldx con la propiedad de no poder ser integrada sin el conocimiento explícito de la relación entre x e y, esto es de y=y(x).

Este resultado lo deduce Euler por reducción al absurdo:

Suponiendo que W no es de la forma antes descrita, será inevitablemente una expresión algebraica, finita o infinita(serie), de x’s, y’s, p’s, q’s, etc.

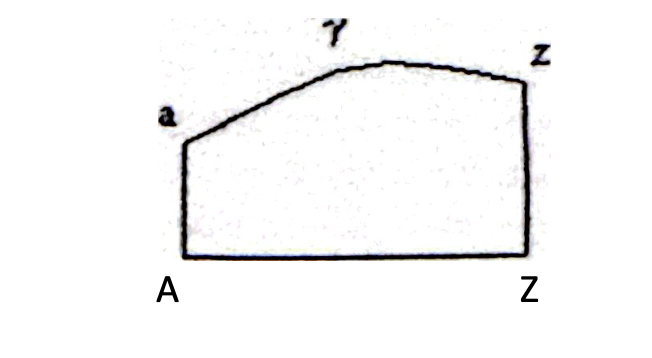
Ahora bien, pongamos por caso que, además de algebraica, W sólo dependiera de x e y; entonces W tomaría el mismo valor para todas las curvas terminadas en zZ, y por tanto, no determinaría la naturaleza de toda la curva en la abscisa AZ. Es decir, que W no diferenciaría entre las curvas a y g:

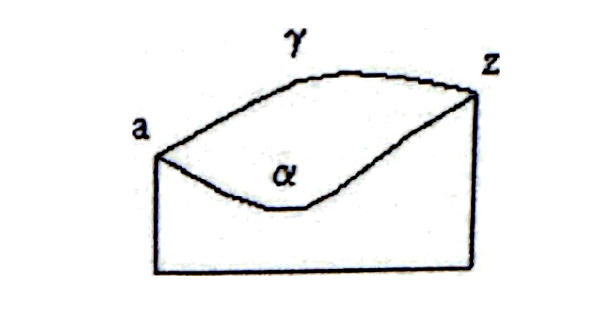
Suponiendo que W dependiera de x, y y p, estaríamos en la situación anterior, quedando, además, fijada la pendiente de las curvas en zZ. Pero seguimos sin eludir la patología del caso anterior.

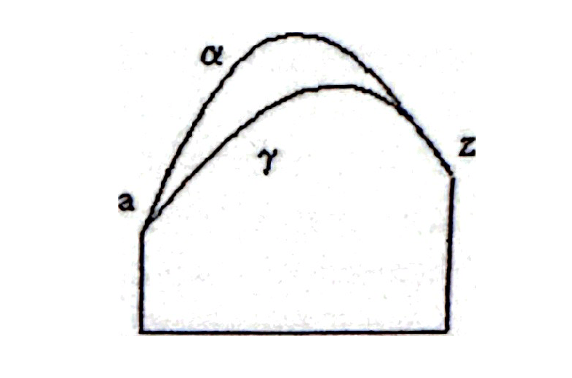
Si W depende de x, y, p y q, quedará, además del punto final y la pendiente, determinada la posición de dos elementos contiguos a la curva en zZ. Y repitiendo este argumento indefinidamente, tendremos, a lo sumo, que W contempla la naturaleza de la curva en un trozo infinitamente pequeño cercano a zZ. Por lo tanto W sigue siendo patológica. Así pues, para que W contemple la naturaleza de la curva en toda la abscisa no le queda más remedio que ser, definitivamente, de la forma  ∫Ldx con las propiedades antes vistas.

Hagamos unas cuantas definiciones importantes de magnitudes referidas a una curva cualquiera: 

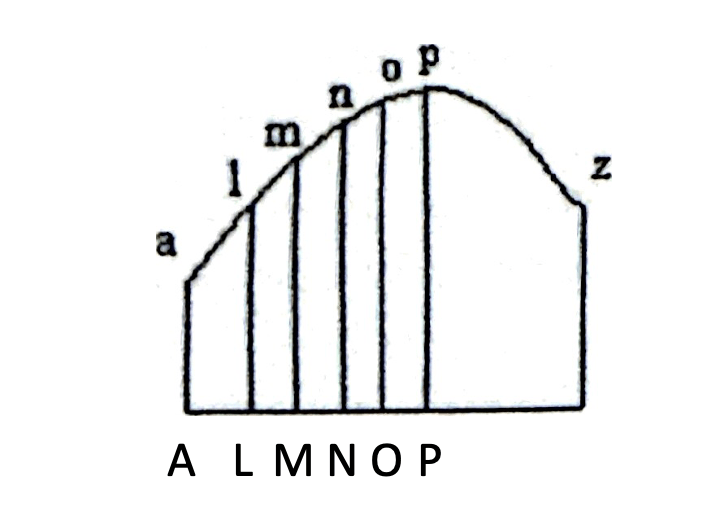
Considerando una partición como en el dibujo anterior, de manera que …, LM, MN, NO, OP, … sean segmentos infinitamente pequeños, definimos por y la ordenada de la abscisa AM = x. Es decir, Mm = y, y definimos Nn=y^I, Oo=y^II,..y Ll=y_I, Kk=y_II, …

Finalmente,

p^I = (y^I – y)/dx , p^II = (y^II – y^I)/dx, … y p_I = (y – y_I)/dx , p_II = (y_I – y_II)/dx, …

de donde,

p = dy/dx = (Nn-Mm)/dx = (y^I – y)/dx

q = dp/dx = (p – p^I)/dx= (y^II – 2y^I + y)/dx

A continuación, expongo una definición que, como veremos, será de gran importancia:

Si  ∫Ldx se refiere a la abscisa x = AM, entonces el valor de esta fórmula en el elemento siguiente MN = dx será Ldx, en NO tendremos L^Idx, … y así sucesivamente de manera que si el valor de   ∫Ldx se refiere a la abscisa AM= x de la curva entonces el valor referido a la abscisa AZ será:

∫Ldx + Ldx + L^Idx +… hacia el infinito hasta llegar a Z.

En consecuencia, el problema de hacer  ∫Ldx máxima o mínima en la abscisa AZ es equivalente a hacer máxima o mínima la expresión ∫Ldx + Ldx + L^Idx +…, con el primer término referido a la abscisa AM.

Una vez terminada la siempre pesada tarea de definir, nada puede ser mejor que demostrar el resultado general que Jakob Bernoulli exponía para el caso concreto de la braquistócrona. Un teorema que nos da un método para hallar las curvas que maximizan o minimizan W y que muestra de forma clarividente la naturaleza de esas curvas.

El pliegue, o el teorema de la variación continua

TEOREMA: «Si amnoz es una Curva referida a la abscisa AZ en la que la fórmula  ∫Ldx toma un valor máximo o mínimo; y se concibe otra curva amvoz que difiera infinitamente poco de la anterior, entonces el valor de la fórmula  ∫Ldx será el mismo para una y otra curva».

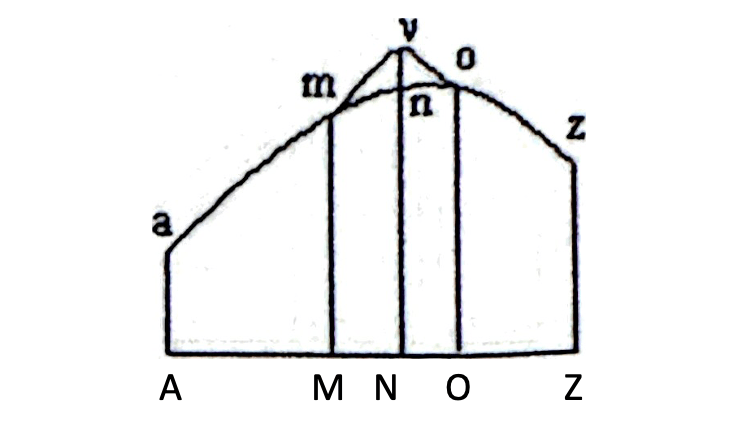
DEMOSTRACIÓN: Considerada una función cualquiera que toma un máximo, sabemos que al acercarnos al máximo continuamente la función crece, y que después, al alejarnos, decrece. Pero lo importante para nuestra proposición es que esos incrementos y esos decrementos al acercarnos y alejarnos al máximo son nulos. Este último razonamiento de Euler es equivalente a decir, tal y como decimos hoy, que la derivada (tasa de cambio de crecimiento y decrecimiento) se hace nula en el máximo.

Por tanto, si  ∫Ldx toma una valor máximo en la curva amnoz, entonces, para una curva amvoz que difiera infinitamente poco de amnoz, es decir, para una variación continua o pliegue, el valor de  ∫Ldx será el mismo puesto que el incremento o decremento será nulo. q.e.d

Es pertinente apuntar aquí la potencialidad con que Euler utiliza el concepto de función en su versión más general. Esto queda manifiesto tanto en esta última demostración, como en la dilucidación de W, el funcional. Si llamamos valor diferencial de W(= ∫Ldx) a la diferencia entre los valores de W en una curva y ésta variada infinitamente poco, obtenemos que, en virtud del teorema, ese valor diferencial en la curva que da máximo o mínimo será nulo. Es decir, y permitiéndonos el lujo de utilizar y abusar de la notación que Lagrange introdujo poco después de editarse el Methodus de Euler, que si consideramos δW=W(amnoz)-W(amvoz), y amnoz es la curva que maximiza o minimiza W, entonces δW=0.

El caso L dependiendo de x, y y p o L (x, y, p)

Sea L una función determinada de x, y y p, de modo que sea dL = Mdx + Ndy+ Pdp; cómo podemos hallar la curva, entre todas las que corresponden a una misma abscisa, en la que  ∫Ldx sea un máximo o un mínimo.

Como hemos visto en el apartado anterior el problema se reducirá a solucionar la ecuación 

δW = δ( ∫Ldx ) = 0

Pero primero vamos a ver de qué manera la pequeña variación nv, a que sometíamos la curva amnoz, hace incrementar o decrementar algunas magnitudes referidas a la curva.

Dado que p = (y^I – y)/dx, para hallar el incremento de esta magnitud no tendremos más que cambiar en ella y^I por y^I+nv, pues y^I+nv no es otra cosa que la ordenada de la curva amvoz correspondiente a la abscisa AN. Obtendremos,

(y^I + nv – y)/dx = (y^I – y)/dx + nv/dx

y por tanto el incremento que apreciará p será nv/dx.

Procediendo de igual manera obtenemos el decremento -nv/dx en p^I.

Los incrementos o decrementos de las magnitudes así obtenidos es lícito considerarlos como los diferenciales de esas mismas magnitudes:

dy^I = nv, dp = nv/dx, …

La forma de calcular el incremento experimentado por una función, por ejemplo y^I(1+p²)^1/2, será diferenciar primero, dy^I(1+p²)^1/2 + y^Ipdp/((1+p²)^1/2, y substituir dy‘ por nv y dp por nv/dx, quedando nv(1+p²)^1/2 + y^Ipnv/dx(1+p²)^1/2.

Ya estamos en condiciones de solucionar el problema:

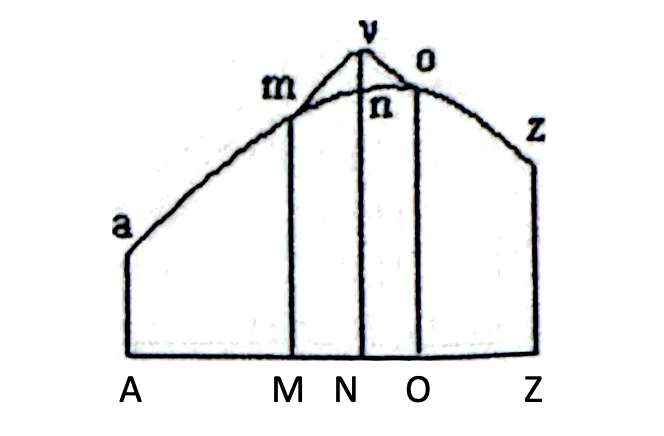
Variada nuestra curva amz el pequeño trozo nv en su ordenada y^I, el valor diferencial de la fórmula  ∫Ldx deberá anularse, o lo que es lo mismo, se anulará el valor diferencial de la fórmula 

…. + L_IIdx + L_Idx + Ldx + L^Idx + L^IIdx +…

Pero como las únicas magnitudes de la curva afectadas por la variación son y^I, p y p^I, sólo se verán afectados los términos Ldx y L^Idx puesto que L depende de x, y y p y L^I de x, y y p^I.

En consecuencia, los términos Ldx y L^Idx serán los únicos que tendremos que diferenciar y realizar el cambio de dy, dp y dp^I, por los incrementos nv, nv/dx, -nv/dx. El resto de términos se anularán mutuamente al realizar la resta que implica el diferencial, pues son iguales para las curvas amnoz y amvoz.

Como dL = Mdx + Ndy+ Pdp y dL^I = M^Idx + N^Idy^I + P^Idp^I, el valor diferencial de L y L^I será respectivamente P (nv/dx) y N^Inv – P^Inv/dx. Y de aquí, fácilmente, el valor diferencial de Ldx + L’dx queda nv(P + Ndx – P^I), pero como dP = P^I– P y en lugar de N^I podemos poner N, resulta nv(Ndx-dP). Igualando a cero queda la ecuación: N – dP/dx = 0.

La curva de más rápido descenso

Dada una abscisa AZ, queremos hallar la curva que, referida a esa abscisa y fijados sus dos extremos, al poner un punto material en su extremo aA llegará en el menor tiempo posible a su otro extremo zZ, suponiendo que no hay rozamiento. Es decir, queremos hallar la curva por la cual un objeto experimentaría el más rápido descenso.

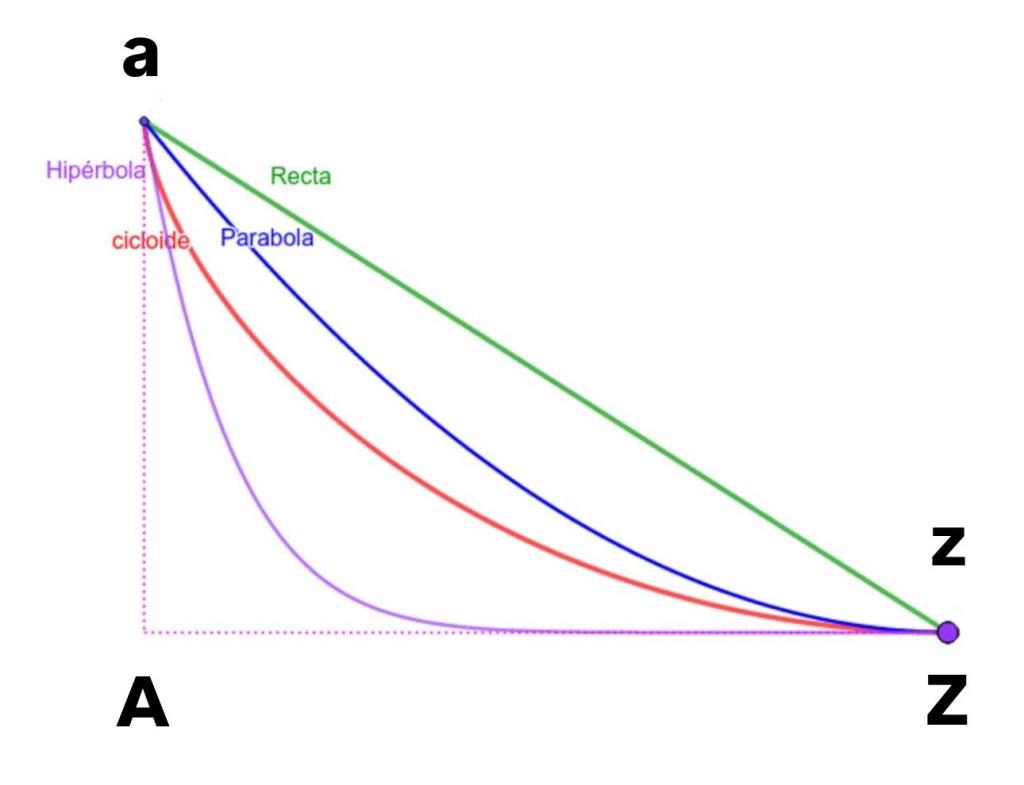
Supondremos gravedad uniforme y el eje de abscisas vertical.

Como se deduce trivialmente de las ecuaciones de movimiento, fijado un punto inicial Aa y una velocidad inicial nula, tendremos que la velocidad instantánea del punto material será ds/dt = (2gx)^1/2, donde s es el arco de curva y ds un diferencial del arco de curva.

Fijémonos también que ds² = dx² + dy² = dx² + p²dx² = (1 + p²) dx².

Llamemos T al tiempo transcurrido en el desplazamiento de Aa a Zz, que es justamente lo que queremos minimizar.

T = ∫dt = ∫ ds/(2gx)^1/2 = ∫(1 + p²) ^1/2/ (2gx)^1/2 dx

Así pues, ya hemos obtenido nuestra fórmula de minimización T, que depende de x, y y p. Por tanto, estamos en la situación del problema anterior para el cual ya habíamos encontrado la ecuación que nos daba la curva solución:

N – dP/dx = 0 

Dado que

L = (1 + p²) ^1/2/ (2gx)^1/2

diferenciando obtenemos,

dL = -[ (1 + p²) ^1/2/ 2x(x)^1/2]dx+ [ p/x(1 + p²)^1/2]dp

Y como,

dL = Mdx + Ndy + Pdp

nos queda,

M = -[ (1 + p²) ^1/2/ 2x(x)^1/2], N = 0, P = [ p/(x(1 + p²)) ^1/2].

Como N = 0, tenemos que la ecuación N – dP/dx = 0 nos queda dP/dx = 0. Lo que implica que P = const = 1/a^1/2 = [ p / (x(1 + p²)) ^1/2]. Si manipulamos esta última igualdad llegamos a ap² = x + p²x, que fácilmente se reduce a p= dy/dx = (x/(a –x))^1/2. 

Y para terminar, integrando a ambos lados, obtenemos la ecuación:

y = ∫ dx (x/(a –x))^1/2

que no es otra cosa que la CICLOIDE.

Inauguración del cálculo de variaciones o ¿la muerte de Dios?

Con esta demostración Euler inauguró el cálculo de variaciones, un logro científico de calado histórico fundamental que posibilitará la mecánica analítica que los físicos utilizan, aún hoy, para desentrañar los misterios cuánticos del universo. Ahora bien, sobre lo que no se ha llamado demasiado la atención es que, mediante esta demostración, la cicloide ya no es la curva que Dios, con su infinita sabiduría, ha preestablecido para optimizar el mundo, sino una curva óptima que se deduce a partir de exigencias estrictamente matemáticas. El gesto de Euler es el de una sustitución brutal gestada en la escritura secular, ilustrada, del matema: el formalismo matemático riguroso viene al lugar de Dios, y a partir de ese preciso momento, la curva única que actualiza la virtualidad variacional de las curvas posibles, no es la rúbrica de un orden divino como creería Leibniz, es la curva que maximiza una simple función matemática W. «¡No veo a tu Dios en mis fórmulas!» increpa Euler a Leibniz, «No vayas tan deprisa Euler, ¿y si Dios era matemático y esa función W y tu formalismo no hace más que traer a escena lo que él ya pensó para ti?» replica un Leibniz avispado, «No sé yo, creo más bien, mi estimado y brillante filósofo, que he sepultado al Dios de tu teodicea entre funciones e integrales» sentencia Euler con ironía.

ENM (2025)