14 de enero de 1978, Kurt Gödel muere de inanición, pesa menos de 30 kilos. La muerte del que fuera el mayor matemático y lógico del siglo XX fue su último teorema: establecidos los axiomas, la muerte no pasó de ser más que la consecuencia directa e irrevocable de la lógica, una descompresión de lo comprimido en una particular axiomática vital. El rigor del matema, del significante puro y sus secuencias lógicas, a las que Gödel debió una fidelidad incondicional a lo largo de toda su vida, decidieron su final trágico. Primer axioma: la fobia, miedo a ser envenenado, un Autre quiere envenenarme. Segundo axioma: sólo la comida elaborada por mi esposa Adele no está envenenada. Dos axiomas delirantes, que duda cabe, pero por poco que pensemos caemos en la cuenta de que todos los axiomas matemáticos lo son: por dos puntos distintos pasa una única recta, dados tres puntos cualesquiera de una recta solo uno puede estar entre los otros dos, etc. ¡Menuda locura! Adele es hospitalizada, no puede preparar la comida. La mente de Gödel inicia el juego implacable de los silogismos: si Adele no puede proporcionarme el alimento, sólo puede llegarme a través de un Autre, ese Autre no es Adele, es el que quiere envenenarme, ergo no puedo comer. Inanición por unos meses, muerte, fin. Q.E.D.
Generalmente se ha ubicado a Gödel dentro del Círculo de Viena, es un craso error, un malentendido atroz, él estuvo presente en algunas de sus reuniones, pero nunca creyó en el positivismo lógico, lo consideraba un engendro pueril y superficial. Lógico, era una persona muy inteligente. Gödel era platónico, defendía un realismo matemático, a saber, que la matemática y la lógica constituyen la esencia última de la realidad, su ontología. Su otra referencia filosófica clave, aparte de Platón claro está, era el genio Leibniz. Soñaba, como el polímata de Leipzig, con una «Characteristica Universalis», con un lenguaje universal cuyos símbolos y reglas lógicas permitirían deducir de forma clara las leyes y el curso íntegro del universo. «Nihil est sine ratione» (nada sin razón) rezaba Leibniz, «ohne zureichenden Grund existiert nichts» (sin una razón suficiente, nada existe) aseveraba Gödel. En una carta de 1967 a su amigo Hao Wang, nuestro lógico matemático sentencia: «El principio de razón suficiente es la piedra angular de la racionalidad. Negarlo sería admitir que el universo es absurdo […] y las matemáticas perderían su objetividad». Lo que no deja de ser paradójico, veremos por qué, es que este sueño loco era también el de otro gran matemático, David Hilbert, el cual, en 1920, propuso a la comunidad matemática internacional el programa de, nada más y nada menos, dar con un sistema de axiomas para las matemáticas que fuera completo y consistente, esto es, propuso el problema de hallar un número finito de verdades matemáticas autoevidentes que comprimieran todo el saber matemático posible (completitud); además, este sistema debía cumplir el requisito de estar exento de contradicción lógica alguna (consistencia).
Gödel qua Leibniz qua Hilbert creían en un Autre completo y consistente. Y además, cosa esta decisiva, el saber acerca de este Autre, el lenguaje y las reglas de nuestro universo, podían escribirse en la forma de un lenguaje universal y absoluto. Tales son las condiciones de un problema postulado bajo la idea, típicamente obsesiva, de la exhaustividad y omnipotencia de la máquina del significante que todo lo cubre, que se arroga el poderío de recubrir y codificar lo real sin falla ni agujero ninguno. Esta posición obsesiva exige, de una parte, un empuje denodado hacia el saber, una voluntad decidida por saber, y de otra, una fidelidad irrestricta al matema, al formulismo matemático y su lógica, acompañada de una rigurosidad y minuciosidad que rayan lo maniático. Una y otra cosa eran cualidades sorprendentes de Gödel: gozar a través del saber, gozar a través de la dinámica fálica de la mecánica simbólica del significante, y todo ello a través de la fantasía de la posibilidad de un universo sin resto, sin falla, sin agujero. Desde Edipo, sabemos que la pulsión de saber (der Wissentrieb) tiene como destino ineludible e inesperado el no-saber, la castración; es más, en una especie de torsión inesperada que Freud identificó certeramente, es este límite constitutivo del saber el que empuja al saber mismo. Estas son las lecciones que nos enseña la tragedia griega: por el anverso, la lealtad al significante lleva al punto en que el significante no alcanza en su decir, y una vez ahí, llegados a ese litoral, ya sólo queda contornear el hueco de lo indecible mismo, es decir, la hiancia; y visto por el reverso, lo indecible, el no-saber, impulsa una estrategia que busca taponar esa grieta mediante el saber. Gödel, muy a pesar suyo, no fue el Leibniz del siglo XX, sino un Edipo más. Para entender este hecho inesperado tenemos que adentrarnos, por fin, en su Teorema de la incompletitud, publicado por él en 1931 bajo el título “Über formal unentscheidbare Sätze der Principia Mathematica und verwandter Systeme I” (Sobre proposiciones formalmente indecidibles de los Principia Mathematica y sistemas relacionados I).

¿Qué dice dicho Teorema? Algo sencillo, pero realmente asombroso, a saber: cualquier sistema de axiomas S que sea consistente y que, además, sea mínimamente expresivo (esto es, que incluya la aritmética básica), es incompleto. En otros términos, para cualquier sistema axiomático S con los requisitos antedichos siempre existen proposiciones verdaderas que dicho sistema no puede demostrar, proposiciones que aun siendo verdaderas son literalmente indecibles a partir de la descompresión lógica de la axiomática misma. ¡Golpe definitivo al “programa” de Hilbert! El optimismo formalista de Hilbert tocaba a su fin, se abría un nuevo periodo caracterizado por la angustia gödeliana. Ya entraremos en las consecuencias de esto para la matemática, para la posición filosófica de Gödel y para Gödel mismo, ya apuntamos la hipótesis de que mucho tendrá que ver con su final trágico; de momento, lo que nos interesa ahora es mostrar cómo la fidelidad irrestricta al procedimiento formal y su lógica, el goce en el automatismo del significante puro, conduce a este singular y sorprendente atolladero. Para demostrar el Teorema de la incompletitud de Gödel vamos a valernos del Teorema de la parada (Halting problem) demostrado por Alan Turing en 1936. De hecho, como señalara el lúcido matemático Gregory Chaitin, la incomputabilidad de Turing implica la incompletitud de Gödel. Ciertamente, no va a ser la demostración que dio Gödel, pero esta es mucho más divertida. Vamos a ello.
Lo primero de lo que hay que percatarse ahora es que nuestra «Characteristica Universalis», ese lenguaje universal hecho de símbolos y reglas, puede pensarse como una máquina de Turing cuyas cadenas significantes sin sentido producen el conjunto de los teoremas matemáticos, y con ello, las leyes y la historia del universo. Sentado esto, vamos con el Teorema de la parada de Turing: No existe un algoritmo H que, para cualquier programa P con una entrada x, pueda predecir si este se detendrá. La demostración de este teorema es sencilla y a la vez muy ingeniosa. Turing la realizó por reducción al absurdo. Partamos, pues, de que existe un programa que puede predecir la parada de P con x, y veamos que esta suposición tiene como consecuencia un absurdo. Sea H ese programa que toma como argumentos P y x. Cuando P con x se detiene tendremos H(P, x)=1 y cuando P con x no se detenga tendremos H(P, x)=0. Y ahora viene lo ingenioso. Turing se inventa una máquina D que va a hacer lo siguiente: si H(P, P)=1, esto es, el programa P se detiene cuando tiene como argumento a sí mismo, entonces D entra en un bucle infinito; si H(P, P)=0, esto es, el programa P no se detiene cuando se tiene a sí mismo como argumento, entonces D se detiene inmediatamente. ¿Qué pasa cuando evaluamos D(D)? ¿Qué ocurre cuando a esta curiosa máquina le pasamos como argumento ella misma? Veamos… Si H(D, D)=1 tenemos que D se detiene (por la definición misma de H), pero, si H(D, D)=1, por la definición de D, tenemos que D entra en bucle infinito. ¡Contradicción! Y si H(D, D)=0 tenemos que D no se para (por la definición de H), pero, a un tiempo, si H(D, D)=0, por la definición de D, tenemos que D se detiene inmediatamente. ¡Contradicción! Conclusión: no existe ese algoritmo H capaz de predecir la parada de un programa cualquiera P con una entrada x, o dicho aún de otra manera, H es incomputable.
Esta demostración puede ilustrarse representando cada programa H, D, etc. como círculos que toman un color verde cuando se detienen y un color rojo cuando entran en un bucle infinito:
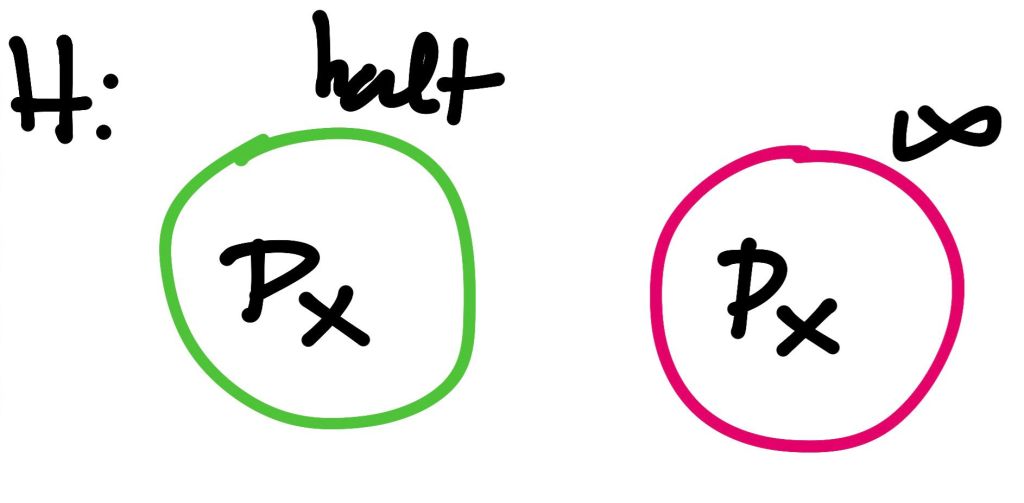
Cuando P con x se detiene, círculo en verde; cuando entra en bucle, círculo en rojo.
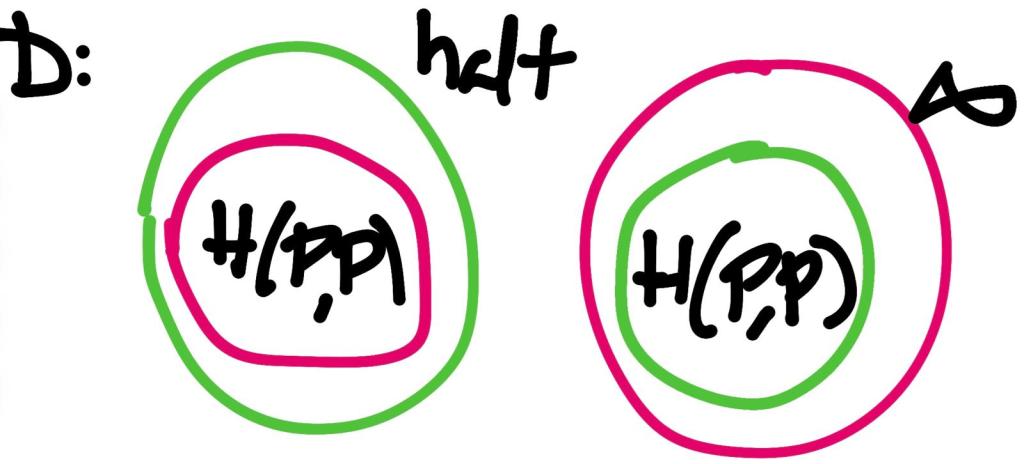
Si P con P no se detiene, H entra en bucle, luego círculo rojo, y bajo esta condición D se para, círculo verde.
Y al contrario, si P con P se detiene, H se detiene, luego círculo verde, y bajo esta condición D entra en bucle infinito, círculo rojo.
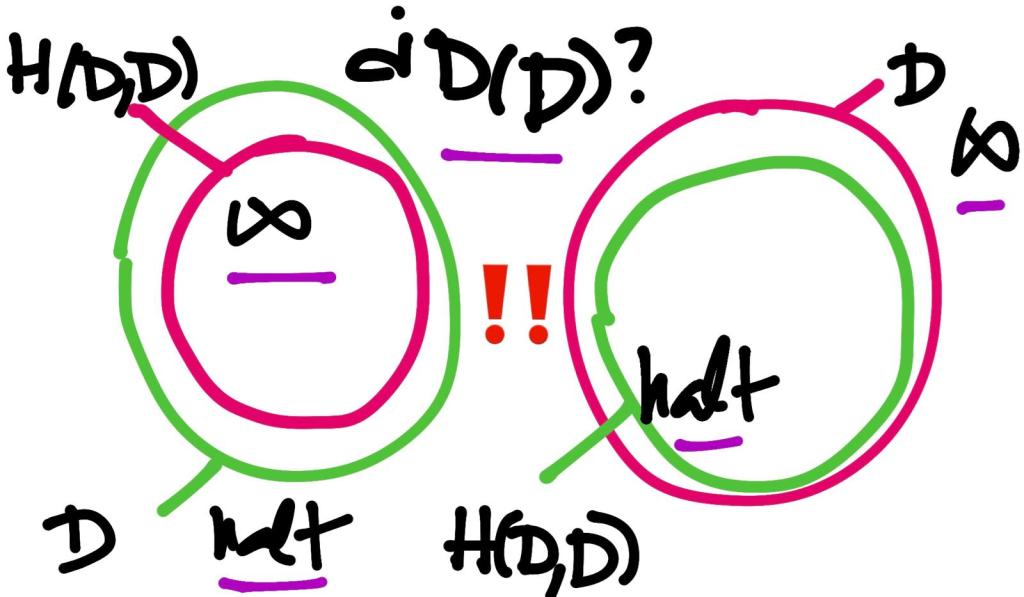
La función diagonal D toma como argumento a D.
Si D entra en bucle entonces H también, círculo rojo. Pero si D entra en bucle, entonces D se detiene, círculo verde. Contradicción.
Si D se detiene entonces H también, círculo verde. Pero si D se detiene, entonces D entra en bucle y no se detiene, círculo rojo. Contradicción
Ahora nos queda mostrar que la incomputabilidad de Turing implica la incompletitud de Gödel. La idea pasa por demostrar que, si existiera un sistema axiomático suficientemente expresivo, consistente y completo, entonces podríamos decidir el problema de la parada de Turing, es decir, podríamos computar una H como la anterior, cosa que, acabamos de ver, ¡es imposible! Si nuestro sistema es completo toda proposición aritmética verdadera es decible, esto es, podrá deducirse a partir de la descompresión de nuestro sistema axiomático S. Hecha esta consideración, entonces para una proposición cualquiera φ, únicamente habremos de esperar a ver si en nuestra descompresión deductiva de los axiomas aparece φ o ¬φ (la negación de φ) para determinar si φ es verdadera o falsa. Postulemos ahora, es una cuestión de traducción, que para cualquier programa P con entrada x tenemos una proposición en S de la forma H(P, x) tal que P con x se detiene si y solo si H(P, x) es verdadera. Con esto ya hemos alcanzado la posibilidad de decidir si se dará la parada de un programa cualquiera P con la entrada x, pues únicamente habremos de ver si en la descompresión de nuestra axiomática S aparece H(P, x) o ¬H(P, x) para decidir si P con x se detiene o no. Ahora bien, esto es justo lo que Turing demostró que era imposible, ergo nuestro sistema no es completo. Q.E.D.
Lo que no debe pasársenos por alto aquí es que nuestra H, la función de parada, siendo estrictamente correlativa de la proposición G de Gödel «esta proposición no es demostrable», es la formalización significante de aquello que no puede incluirse en el automatismo del significante que se despliega a partir de la axiomática S. Lo que la máquina significante de Turing no puede calcular es, en suma, el lugar del goce que excede el falo. Dicho en términos lacanianos, tanto H como G son a S lo que el significante de la castración S(Ⱥ) es al Autre. El problema de la parada de Turing y el teorema de la incompletitud de Gödel alcanzan lo litoral, el punto mismo en el que lo posible y necesario del goce fálico a través del matema, de la formalización matemática mediante el significante puro, arriba al lugar imposible de la letra donde se abre lo oceánico de un goce autre, ilimitado. ¿A dónde llegó pues Gödel? A que el Autre es no-todo, que está agujerado, que es incompleto. El saber en Gödel, su convicción en un platonismo matemático y en un idioma absoluto a lo Leibniz, era una defensa contra la castración, su particular manera de negarse a ver la falta en el Autre y en uno mismo; pero, lo realmente paradójico, es que en su actividad matemática denodada derivada de su pasión por saber acabó dándose de bruces, como Edipo, con el no-saber de la castración. Y es que la verdad excede el saber… ¿Aceptó este hecho Gödel? En absoluto, el obsesivo no tolera el agujero, el no-saber es la ocasión para relanzarse en la búsqueda del saber y rearmar la fantasía de un Autre completo y omnipotente. Qué sufrimiento… La artimaña filosófica de Gödel no se hizo esperar: su Teorema de la incompletitud únicamente ponía de relieve las limitaciones del conocimiento, de la matemática y de la lógica producidas por la mente humana, pero su realismo platónico matemático quedaba indemne. Curiosa aporía la de Gödel, pues si la matemática tiene un estatuto de realidad -esto y ninguna otra cosa es ser realista platónico en matemáticas-, su teorema de incompletitud no podía sino ser índice de una incompletitud en la realidad misma, en el Autre.

Gödel, lo hemos dicho ya, era sumamente inteligente, luego no pudo escapársele, o como mínimo seguro que le preocupó sobremanera, que sus argumentos tuvieran toda la pinta de ser meras argucias filosóficas. 1951 es un año que nos brinda un síntoma sumamente clarificador a este respecto. Gödel, durante su examen de nacionalidad estadounidense, argumenta al juez que la Constitución de los Estados Unidos tiene contradicciones internas capaces de legitimar una dictadura. Sus amigos Albert Einstein y Oskar Morgenstern tuvieron que detenerlo para evitar que arruinara el trámite. Lo lógico se deslizaba hacia lo delirante, la misma inteligencia que descubrió la falla estructural de los sistemas formales matemáticos, empieza a encontrar contradicciones en el mundo político, en la medicina, etc. En los años sesenta y setenta, el delirio se consolida, Gödel percibe el Instituto de Estudios Avanzados de Princeton como un lugar de complots en su contra. El mal estaba hecho: el Autre completo no existe, no todo puede decirse, no todo puede saberse, no todo está legislado bajo el universo simbólico, no hay metalenguaje; lo que hay es ¡castración! Toda esta lógica subyacente a Gödel sintomatiza su posición subjetiva. Lo que es decisivo es que la fragilidad de la estructura subjetiva de Gödel sólo pudo salvar este atolladero mediante lo que Freud denominó «ein Ersatz»: inventando una sustitución, como en el caso de Ernst Lanzer, el hombre de las ratas (der Rattenmann). Al lugar que ocupaba la fantasía, ahora fracasada, de la «Characteristica Universalis» que otrora tapaba el agujero en el Autre, vino la fobia del envenenamiento. El Autre ya no era de fiar, no se podía controlar, había que defenderse de ese goce autre no sujeto a la legalidad fálica del matema, y esta defensa se armó en base a la particular fobia de un Autre que quería asesinarlo envenenándolo… Leibniz soñó con el mejor de los mundos posibles; Lacan nos enseña que no hay mundo sin pérdida, y Gödel murió por no ceder ese resto. La muerte por inanición no fue más que una expresión de la imposibilidad de confiar en ese Autre. Paradojas de la historia que, una vez más, evocan a Edipo en Colona: el último teorema de Gödel, su muerte, es el corolario final del teorema de incompletitud que lo hizo inmortal.
«La idea de Leibniz de una «characteristica universalis» no era una fantasía utópica, sino más bien una intuición profunda sobre la naturaleza misma del conocimiento. Es tarea de la filosofía descubrir los conceptos fundamentales que gobiernan el universo, y semejante lenguaje sería la expresión última de esta racionalidad.»
– Kurt Gödel, en carta a su madre de 1961
ENM (2025)




